题目内容
13.放学以后,小明和小华从学校分开,分别向北和东走回家,若小明和小华行走的速度都是50米/分,小明用10分到家,小华用24分到家,小明和小华家的距离为( )| A. | 600米 | B. | 800米 | C. | 1000米 | D. | 1300米 |
分析 根据题意画出图形,再根据勾股定理求解即可.
解答  解:如图所示,
解:如图所示,
∵小明用10分到家,小华用24分到家,
∴OA=10×50=500(米),OB=24×50=1200(米),
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=1300(米).
答:小明和小华家的距离为1300米.
故选:D.
点评 本题考查的是勾股定理的应用,熟知在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
4.下列抽样方法是随机抽样的是( )
| A. | 为了解刚生产的零件的质量情况,从每一个包装箱内抽5个加以检查 | |
| B. | 为了解全市学生的身高情况,以一、三中的学生为代表进行考察 | |
| C. | 为了解小学生的视力情况,选中六年级20名学生进行调查 | |
| D. | 为了解某地区的车流量,记录某一红绿灯处早上8:00至9:00的车流量 |
1.在般市交易中,假设卖一次股票需付交易款的千分之三作为税金,某投资者在上周最后一个交易日以每股30元的价格买入某股票1000股,下表为本周内每日该股票的涨跌情况(单位:元)
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少?最低价是多少元?
(3)若他在周五全部卖出,收益如何?
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 涨跌 | -1 | +2.5 | -0.5 | -1.5 | +2 |
(2)本周内每股最高价是多少?最低价是多少元?
(3)若他在周五全部卖出,收益如何?
3. 一种足球是由32块黑白相间的牛皮缝制而成的(如图,黑皮可看做正五边形,白皮可看做正六边形).设黑皮有x块,则白皮有(32-x)块.下面所列的方程正确的是( )
一种足球是由32块黑白相间的牛皮缝制而成的(如图,黑皮可看做正五边形,白皮可看做正六边形).设黑皮有x块,则白皮有(32-x)块.下面所列的方程正确的是( )
 一种足球是由32块黑白相间的牛皮缝制而成的(如图,黑皮可看做正五边形,白皮可看做正六边形).设黑皮有x块,则白皮有(32-x)块.下面所列的方程正确的是( )
一种足球是由32块黑白相间的牛皮缝制而成的(如图,黑皮可看做正五边形,白皮可看做正六边形).设黑皮有x块,则白皮有(32-x)块.下面所列的方程正确的是( )| A. | 3(32-x)=x | B. | 3(32-x)=5x | C. | 5(32-x)=3x | D. | 6(32-x)=x |
 桌面上放着两个物体,分别从它们的正面、左面、上面三个方向看到的图形如图,则这两个物体分别是长方体和圆柱,它们的位置是圆柱前长方体后.
桌面上放着两个物体,分别从它们的正面、左面、上面三个方向看到的图形如图,则这两个物体分别是长方体和圆柱,它们的位置是圆柱前长方体后. 如图所示,求出图中x的值.
如图所示,求出图中x的值.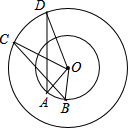 如图,点A,B和点C,D分别在两个同心圆上,且∠AOB=∠COD.求证:∠C=∠D.
如图,点A,B和点C,D分别在两个同心圆上,且∠AOB=∠COD.求证:∠C=∠D.