Question

2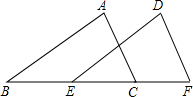．如图，在△ABC和△DEF中，B，E，C，F在同一条直线上，下面有四个条件：①AB=DE，②AC=DF，③∠ABC=∠DEF，④BE=CF．请你在其中选3个作为题设，余下的1个作为结论，写出所有能组成真命题组合的题设为①②④或①③④．（填序号）

Answer 1

分析 直接利用全等三角形的判定方法分别得出符合题意的答案．

解答 解：∵BE=CF，
∴BC=EF，
在△ABC和△DEF中
∵$\left\{\begin{array}{l}{AB=DE}\\{∠ABC=∠DEF}\\{BC=EF}\end{array}\right.$，
∴△ABC≌△DEF（SAS），
∴AC=DF，
即①③④为题设，可以得出②；
∵BE=CF，
∴BC=EF，
在△ABC和△DEF中
∵$\left\{\begin{array}{l}{AB=DE}\\{AC=DF}\\{BC=EF}\end{array}\right.$，
∴△ABC≌△DEF（SSS），
∴∠ABC=∠DEF，
即①②④为题设，可以得出③；
故答案为：①②④或①③④．

点评 此题主要考查了命题与定理，正确掌握全等三角形的判定方法是解题关键．