题目内容
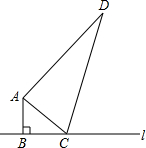 如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.
如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.考点:勾股定理的逆定理
专题:
分析:设BC=xcm,则CD=(34-x)cm,再根据勾股定理及勾股定理的逆定理列出方程,求出x的值即可.
解答:解:∵BC与CD的长度之和为34cm,
∴设BC=xcm,则CD=(34-x)cm.
∵在△ABC中,∠ABC=90°,AB=6cm,
∴AC2=AB2+BC2=62+x2.
∵△ACD是以DC为斜边的直角三角形,AD=24cm,
∴AC2=CD2-AD2=(34-x)2-242,
∴62+x2=(34-x)2-242,
解得x=8,
即BC=8cm.
答:当C离点B8cm时,△ACD是以DC为斜边的直角三角形.
∴设BC=xcm,则CD=(34-x)cm.
∵在△ABC中,∠ABC=90°,AB=6cm,
∴AC2=AB2+BC2=62+x2.
∵△ACD是以DC为斜边的直角三角形,AD=24cm,
∴AC2=CD2-AD2=(34-x)2-242,
∴62+x2=(34-x)2-242,
解得x=8,
即BC=8cm.
答:当C离点B8cm时,△ACD是以DC为斜边的直角三角形.
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EH=FG,②EH=HG,③四边形EFGH是菱形,④EG⊥FH.其中正确的个数是( )
如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EH=FG,②EH=HG,③四边形EFGH是菱形,④EG⊥FH.其中正确的个数是( ) 如图,⊙O中的弦AB,CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2
如图,⊙O中的弦AB,CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2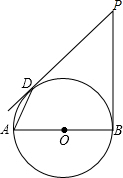 已知:PB切⊙O于B,AB为⊙O的直径,PO∥AD,求证:PD为⊙O的切线.
已知:PB切⊙O于B,AB为⊙O的直径,PO∥AD,求证:PD为⊙O的切线.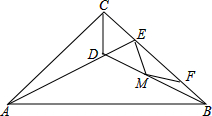 如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠CAD=∠CBD=15°,延长AD交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠CAD=∠CBD=15°,延长AD交BC于点E. 按要求作图:平面上有A,B,C三点,如图所示,画直线AC,射线BC,线段AB,在射线BC上取点D,使BD=AB.
按要求作图:平面上有A,B,C三点,如图所示,画直线AC,射线BC,线段AB,在射线BC上取点D,使BD=AB. 如图,已知正方形ABCD中,点E为BC边上一点,BE=1,tan∠BAE=
如图,已知正方形ABCD中,点E为BC边上一点,BE=1,tan∠BAE=