题目内容
已知A，B是两个锐角，且满足sin2A+cos2B=
t，cos2A+sin2B=
t2，则实数t所有可能值的和为（ ）
| 5 |
| 4 |
| 3 |
| 4 |
分析：根据公式sin2α+cos2α=1列出关于未知数t的一元二次方程，然后根据根与系数的关系解答．
解答：解：根据已知，得
sin2A+cos2B+cos2A+sin2B=
t2+
t，即2=
t2+
t，
∴3t2+5t-8=0，
∴解得t1=1，t2=-
，
又∵sin2A+cos2B=
t＞0，即t＞0，
∴t2=-
不符合题意舍去，
∴t所有可能值的和为1．
故选C．
sin2A+cos2B+cos2A+sin2B=
| 3 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
∴3t2+5t-8=0，
∴解得t1=1，t2=-
| 8 |
| 3 |
又∵sin2A+cos2B=
| 5 |
| 4 |
∴t2=-
| 8 |
| 3 |
∴t所有可能值的和为1．
故选C．
点评：本题主要考查了同角三角函数的关系及根与系数的关系．解答此题的关键是熟练掌握同角三角函数的关系：sin2α+cos2α=1．
练习册系列答案
名校课堂系列答案
相关题目
，
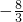
，则实数t所有可能值的和为
，
，则实数t所有可能值的和为（ ）
，
，则实数t所有可能值的和为（ ）
