题目内容
7.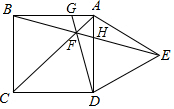 如图,在边长为6的正方形ABCD的外侧作等边△ADE,连接BE交AC于点F,连接DF并延长交AB于点G,则AG的长为( )
如图,在边长为6的正方形ABCD的外侧作等边△ADE,连接BE交AC于点F,连接DF并延长交AB于点G,则AG的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 6$\sqrt{2}$-6 | D. | 12-6$\sqrt{3}$ |
分析 连接BD,交AC于点O,根据正方形的性质得到BD=6$\sqrt{2}$,OB=3$\sqrt{2}$,根据等边三角形的性质得到AE=AD,∠DAE=60°,根据等腰三角形的性质得到∠ABE=∠ABE=15°,求得∠FBO=30°,根据相似三角形的性质即可得到结论.
解答  解:连接BD,交AC于点O,
解:连接BD,交AC于点O,
∵四边形ABCD是正方形,BC=6,
∴BD=6$\sqrt{2}$,
∴OB=3$\sqrt{2}$,
∵△ADE是等边三角形,
∴AE=AD,∠DAE=60°,
∴AB=AE,∠BAE=150°,
∴∠ABE=∠ABE=15°,
∴∠FBO=30°,
∴OF=$\frac{\sqrt{3}}{3}$OB=$\sqrt{6}$,AF=3$\sqrt{2}$-$\sqrt{6}$,CF=3$\sqrt{2}$+$\sqrt{6}$,
∵AB∥CD,
∴△AFG∽△CFD,
∴$\frac{AF}{CF}$=$\frac{AG}{CD}$,即$\frac{3\sqrt{2}-\sqrt{6}}{3\sqrt{2}+\sqrt{6}}$=$\frac{AG}{6}$,
解之,得AG=12-6$\sqrt{3}$.
故选D.
点评 本题考查了正方形的性质,等边三角形的性质,相似三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若关于x的不等式组$\left\{\begin{array}{l}{\frac{x+6}{5}>\frac{x}{4}+1}\\{x+m<0}\end{array}\right.$的解集为x<4,则m的取值范围是( )
| A. | m=-4 | B. | m=4 | C. | m≥4 | D. | m≤-4 |
16.在平行四边形ABCD中,∠A=35°,则∠C大小是( )
| A. | 35° | B. | 55° | C. | 135° | D. | 145° |
17.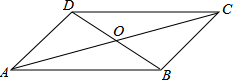 如图,在四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
如图,在四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
 如图,在四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
如图,在四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )| A. | AB∥DC,AD=BC | B. | AD∥BC,AB∥DC | C. | AB=DC,AD=BC | D. | OA=OC,OB=OD |