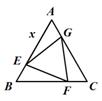
题目内容
已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.

解:(1)如图①,连接OQ.
∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,
∴OQ⊥OP.
又∵BP=OB=OQ=2,
∴PQ= =
= =2
=2 ,即PQ=2
,即PQ=2 ;
;
(2)OQ⊥AC.理由如下:
如图②,连接BC.
∵BP=OB,
∴点B是OP的中点,
又∵PC=CQ,
∴点C是PQ的中点,
∴BC是△PQO的中位线,
∴BC∥OQ.
又∵AB是直径,
∴∠ACB=90°,即BC⊥AC,
∴OQ⊥AC.
(3)如图②,PC•PQ=PB•PA,即 PQ2=2×6,
PQ2=2×6,
解得PQ=2 .
.



练习册系列答案
相关题目
 B. 3
B. 3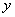 轴对称的△A1B1C1,直接写出点A1的坐标____________.
轴对称的△A1B1C1,直接写出点A1的坐标____________. (3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π). = .
= . ,并把解集在数轴
,并把解集在数轴 上表示出来.
上表示出来.