题目内容
设抛物线y=ax2+bx+c（a≠0）过A（0，2），B（4，3），C三点，其中点C在直线x=2上，且点C到抛物线的对称轴的距离等于1，则抛物线的函数解析式为
y=
x2﹣
x+2或y=﹣
x2+
x+2 ．
解：∵点C在直线x=2上，且到抛物线的对称轴的距离等于1，
∴抛物线的对称轴为直线x=1或x=3，
当对称轴为直线x=1时，设抛物线解析式为y=a（x﹣1）2+k，
将A（0，2），B（4，3）代入解析式，
则
，
解得
，
所以，y=（x﹣1）2+
=x2﹣
x+2；
当对称轴为直线x=3时，设抛物线解析式为y=a（x﹣3）2+k，
将A（0，2），B（4，3）代入解析式，
则
，
解得
，
所以，y=﹣
（x﹣3）2+
=﹣x2+
x+2，
综上所述，抛物线的函数解析式为y=
x2﹣
x+2或y=﹣x2+
x+2．
练习册系列答案
相关题目
（a≠0）在同一平面直角坐标系中的图象可能是（ ）
B．
C．
D． 
位得到的新抛物线恰好经过点B，求新抛物线的解析式；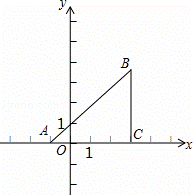
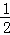，且经过点（2，0），下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（﹣2，y1），（
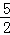，y2）是抛物线上的两点，则y1＜y2，其中说法正确的是（ ）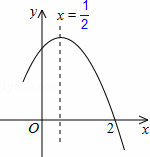
]．
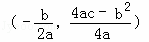