题目内容
如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(﹣1,0),B(m,n),C(3,0).若抛物线y=ax2+bx﹣3经过A、C两点.
(1)求a、b的值;
(2)将抛物线向上平移若干个单 位得到的新抛物线恰好经过点B,求新抛物线的解析式;
位得到的新抛物线恰好经过点B,求新抛物线的解析式;
(3)设(2)中的新抛物的顶点P点,Q为新抛物线上P点至B点之间的一点,以点Q为圆心画图,当⊙Q与x轴和直线BC都相切时,联结PQ、BQ,求四边形ABQP的面积.
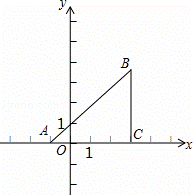
解:(1)∵抛物线y=ax2+bx﹣3经过A(﹣1,0)、C(3,0),
∴ ,
,
解得: ;
;
(2)设抛物线向上平移k个单位后得到的新抛物线恰好经过点B,
则新抛物线的解析式为y=x2﹣2x﹣3+k,
∵A(﹣1,0)、C(3,0),
∴CB=AC=3﹣(﹣1)=4,
∵∠ACB=90°,∴点B的坐标为(3,4).
∵点B(3,4)在抛物线y=x2﹣2x﹣3+k上,
∴9﹣6﹣3+k=4,
解得:k=4,
∴新抛物线的解析式为y=x2﹣2x+1;
(3)设⊙Q与x轴相切于点D,与直线BC相切于点E,连接QD、QE,如图所示,
则有QD⊥OC,QE⊥BC,QD=QE,
∴∠QDC=∠DCE=∠QEC=90°,
∴四边形QECD是矩形.
∵QD=QE,
∴矩形QECD是正方形,
∴QD=DC.
设点Q的横坐标为t,
则有OD=t,QD=DC=OC﹣OD=3﹣t,
∴点Q的坐标为(t,3﹣t).
∵点Q在抛物线y=x2﹣2x+1上,
∴t2﹣2t+1=3﹣t,
解得:t1=2,t2=﹣1.
∵Q为抛物线y=x2﹣2x+1上P点至B点之间的一点,
∴t=2,点Q的坐标为(2,1),
∴OD=2,QD=CD=1.
由y=x2﹣2x+1=(x﹣1)2得顶点P的坐标为(1,0),
∴OP=1,PD=OD﹣OP=2﹣1=1,
∴S四边形ABQP=S△ACB﹣S△PDQ﹣S梯形DQBC
= AC•BC﹣
AC•BC﹣ PD•QD﹣
PD•QD﹣ (QD+BC)•DC
(QD+BC)•DC
= ×4×4﹣
×4×4﹣ ×1×1﹣
×1×1﹣ ×(1+4)×1
×(1+4)×1
=5,
∴四边形ABQP的面积为5.


 颗,会剩余80颗,后来因经费不足少订了2盒,于是改成每人分12颗,但最后分到小佳时巧克力不够分,只有小佳拿不到12颗,但她仍分到3颗以上(含3颗).请问所有可能的工作人员人数为何?请完整写出你的解题过程及所有可能的答案.
颗,会剩余80颗,后来因经费不足少订了2盒,于是改成每人分12颗,但最后分到小佳时巧克力不够分,只有小佳拿不到12颗,但她仍分到3颗以上(含3颗).请问所有可能的工作人员人数为何?请完整写出你的解题过程及所有可能的答案.
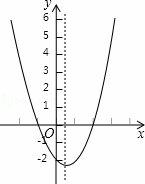
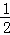 C. 当x<
C. 当x<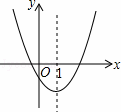

 ,﹣1)、C(﹣
,﹣1)、C(﹣