题目内容
【题目】已知二次函数y=﹣x2+bx+c+1,
①当b=1时,求这个二次函数的对称轴的方程;
②若c= ![]() b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
③若二次函数的图象与x轴交于点A(x1 , 0),B(x2 , 0),且x1<x2 , 与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足 ![]() =
= ![]() ,求二次函数的表达式.
,求二次函数的表达式.
【答案】解:①二次函数y=﹣x2+bx+c+1的对称轴为x= ![]() ,
,
当b=1时, ![]() =
= ![]() ,
,
∴当b=1时,求这个二次函数的对称轴的方程为x= ![]() .
.
②二次函数y=﹣x2+bx+c+1的顶点坐标为( ![]() ,
, ![]() ),
),
∵二次函数的图象与x轴相切且c= ![]() b2﹣2b,
b2﹣2b,
∴ 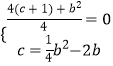 ,解得:b=2+
,解得:b=2+ ![]() 或b=2﹣
或b=2﹣ ![]() ,
,
∴b为2+ ![]() 或2﹣
或2﹣ ![]() 时,二次函数的图象与x轴相切.
时,二次函数的图象与x轴相切.
③∵AB是半圆的直径,
∴∠AMB=90°,
∴∠OAM+∠OBM=90°,
∵∠AOM=∠MOB=90°,
∴∠OAM+∠OMA=90°,
∴∠OMA=∠OBM,
∴△OAM∽△OMB,
∴ ![]() ,
,
∴OM2=OAOB,
∵二次函数的图象与x轴交于点A(x1 , 0),B(x2 , 0),
∴OA=﹣x1 , OB=x2 , x1+x2 , =b,x1x2=﹣(c+1),
∵OM=c+1,
∴(c+1)2=c+1,
解得:c=0或c=﹣1(舍去),
∴c=0,OM=1,
∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足 ![]() =
= ![]() ,
,
∴AD=BD,DF=4DE,
DF∥OM,
∴△BDE∽△BOM,△AOM∽△ADF,
∴ ![]() ,
, ![]() ,
,
∴DE= ![]() ,DF=
,DF= ![]() ,
,
∴ ![]() ×4,
×4,
∴OB=4OA,即x2=﹣4x1 ,
∵x1x2=﹣(c+1)=﹣1,
∴ ![]() ,解得:
,解得: 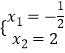 ,
,
∴b=﹣ ![]() +2=
+2= ![]() ,
,
∴二次函数的表达式为y=﹣x2+ ![]() x+1.
x+1.
【解析】①二次函数y=﹣x2+bx+c+1的对称轴为x= ![]() ,即可得出答案;②二次函数y=﹣x2+bx+c+1的顶点坐标为(
,即可得出答案;②二次函数y=﹣x2+bx+c+1的顶点坐标为( ![]() ,
, ![]() ),y由二次函数的图象与x轴相切且c=
),y由二次函数的图象与x轴相切且c= ![]() b2﹣2b,得出方程组
b2﹣2b,得出方程组 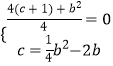 ,求出b即可;③由圆周角定理得出∠AMB=90°,证出∠OMA=∠OBM,得出△OAM∽△OMB,得出OM2=OAOB,由二次函数的图象与x轴的交点和根与系数关系得出OA=﹣x1 , OB=x2 , x1+x2 , =b,x1x2=﹣(c+1),得出方程(c+1)2=c+1,得出c=0,OM=1,证明△BDE∽△BOM,△AOM∽△ADF,得出
,求出b即可;③由圆周角定理得出∠AMB=90°,证出∠OMA=∠OBM,得出△OAM∽△OMB,得出OM2=OAOB,由二次函数的图象与x轴的交点和根与系数关系得出OA=﹣x1 , OB=x2 , x1+x2 , =b,x1x2=﹣(c+1),得出方程(c+1)2=c+1,得出c=0,OM=1,证明△BDE∽△BOM,△AOM∽△ADF,得出 ![]() ,
, ![]() ,得出OB=4OA,即x2=﹣4x1 , 由x1x2=﹣(c+1)=﹣1,得出方程组
,得出OB=4OA,即x2=﹣4x1 , 由x1x2=﹣(c+1)=﹣1,得出方程组 ![]() ,解方程组求出b的值即可.
,解方程组求出b的值即可.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案