Question

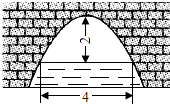
【题目】如图，AB是⊙O的直径，弦CD⊥AB，∠C=30°，CD=2 ．则S阴影=（ ）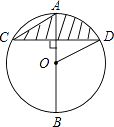
A.π
B.2π
C.
D. π

Answer 1

【答案】D
【解析】 解：∵CD⊥AB，CD=2
∴CE=DE= CD= ，
在Rt△ACE中，∠C=30°，
则AE=CEtan30°=1，
在Rt△OED中，∠DOE=2∠C=60°，
则OD= =2，
∴OE=OA﹣AE=OD﹣AE=1，
S阴影=S扇形OAD﹣S△OED+S△ACE= ﹣ ×1× + ×1× = ．
故选D．
根据垂径定理求得CE=ED= ；然后由圆周角定理知∠AOD=60°，然后通过解直角三角形求得线段AE、OE的长度；最后将相关线段的长度代入S阴影=S扇形OAD﹣S△OED+S△ACE ．