题目内容
如图,抛物线 与
与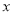 轴正半轴交于点A(3,0).以OA为边在
轴正半轴交于点A(3,0).以OA为边在 轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则
轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则 = ,点E的坐标是 .
= ,点E的坐标是 .

 ;(1+
;(1+ ,1+
,1+ )
)
【解析】
试题分析:把点A(3,0)代入抛物线 ,即可求得a的值,正方形OABC可得点C坐标,代入函数解析式求得点D坐标,可知点E横坐标,再利用正方形BDEF的性质得出点E纵坐标问题得解.
,即可求得a的值,正方形OABC可得点C坐标,代入函数解析式求得点D坐标,可知点E横坐标,再利用正方形BDEF的性质得出点E纵坐标问题得解.
试题解析:把点A(3,0)代入抛物线 ,
,
解得a= ;(1+
;(1+ ,1+
,1+ ).
).
∵四边形OABC为正方形,
∴点C的坐标为(0,3),点D的纵坐标为3,
代入y= x2-x-
x2-x- ,
,
解得x1=1+ ,x2=1-
,x2=1- (不合题意,舍去),
(不合题意,舍去),
因此正方形BDEF的边长B为1+ -3=
-3= -2,
-2,
所以AF=3+ -2=1+
-2=1+ ,
,
由此可以得出点E的坐标为(1+ ,1+
,1+ ).
).
考点:二次函数综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为实数,且满足
为实数,且满足 ,则
,则 的值为( )
的值为( ) B、
B、 C、
C、 D、无解
D、无解 的部分图象如图所示,当
的部分图象如图所示,当 ,则
,则 的取值范围是( )
的取值范围是( )
 B.
B.
 或
或 D.
D. 或
或
 的图象的对称轴是( )
的图象的对称轴是( ) =-2 B.直线
=-2 B.直线 =2 C.直线
=2 C.直线 的开口方向 ,对称轴是 ,顶点坐标是 .
的开口方向 ,对称轴是 ,顶点坐标是 . ,则:
,则:  = ,
= , = .在此条件下,计算:
= .在此条件下,计算:



 = .
= . 的一次项系数是-4
的一次项系数是-4