题目内容
当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为
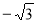 或2
或2
【解析】
试题分析:二次函数y=-(x-m)²+m²+1的顶点为(m,m²+1),
(1)当m<-2时,顶点(对称轴 x=m)在-2≤x≤1范围左侧,此时函数在-2≤x≤1范围内y随着x的增大而减小,所以当x=-2时,y最大,所以4=-(-2-m)²+m²+1,解得m=-7/4,因m<-2,所以m=-7/4舍去;
(2)当-2≤m≤1时,顶点(对称轴 x=m)在-2≤x≤1范围内,所以当x=m时,y有最大值,所以4=m²+1解得:m=±√3,因-2≤m≤1,所以m=√3舍去,所以m=-√3;
(3)当m>1时,顶点(对称轴 x=m)在-2≤x≤1范围右侧,此时函数在-2≤x≤1范围内y随着x的增大而增大,所以当x=1时,y最大,所以4=-(1-m)²+m²+1,解得m=2,
综上得当m=-√3或m=2时,二次函数y=-(x-m)²+m²+1在-2≤x≤1范围内有最大值时4.
考点:1.二次函数的性质;2.二次函数的最值.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 ,求
,求 的值。
的值。 得
得  即
即 
 , 所以
, 所以 
 ,求
,求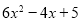 的值。
的值。
 和一次函数
和一次函数 的图象,观察图象写出
的图象,观察图象写出 时,x的取值范围________.
时,x的取值范围________.

 的图象在第二象限的一点,AB⊥
的图象在第二象限的一点,AB⊥ 轴于点B,且
轴于点B,且 =3,则
=3,则 为 .
为 . 与
与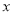 轴正半轴交于点A(3,0).以OA为边在
轴正半轴交于点A(3,0).以OA为边在 轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则
轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则 = ,点E的坐标是 .
= ,点E的坐标是 .
 的“F运算”:①当
的“F运算”:①当 ×
× ×
×