题目内容
 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)△ABC的面积;
(2)边AC的长;
(3)点B到AC边的距离.
解(1)S△ABC=3×3-( ×3×1+
×3×1+ ×2×1+
×2×1+ ×2×3)=
×2×3)= ;
;
(2)AC= =
= ;
;
(3)设点B到AC边的距离为h,则S△ABC= ×AC×h=
×AC×h= ,
,
解得:h=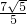 .
.
分析:(1)利用三角形所在的正方形面积减三个小直角三角形的面积即可求出;
(2)利用勾股定理即可求出AC的长;
(3)求出AC,则点B到AC边的距离即为AC边上的高,利用面积定值即可求出.
点评:本题考查了直角三角形面积的计算,正方形各边相等的性质和勾股定理的运用,本题中,正确的运用面积加减法计算结果是解题的关键.
 ×3×1+
×3×1+ ×2×1+
×2×1+ ×2×3)=
×2×3)= ;
;(2)AC=
 =
= ;
;(3)设点B到AC边的距离为h,则S△ABC=
 ×AC×h=
×AC×h= ,
,解得:h=
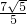 .
.分析:(1)利用三角形所在的正方形面积减三个小直角三角形的面积即可求出;
(2)利用勾股定理即可求出AC的长;
(3)求出AC,则点B到AC边的距离即为AC边上的高,利用面积定值即可求出.
点评:本题考查了直角三角形面积的计算,正方形各边相等的性质和勾股定理的运用,本题中,正确的运用面积加减法计算结果是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,方格纸中小正方形的边长为1,A、B、C都在格点上,求:
如图,方格纸中小正方形的边长为1,A、B、C都在格点上,求: 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求: 如图,方格纸中小正方形的边长为1,A、B、C都在格点上,求:
如图,方格纸中小正方形的边长为1,A、B、C都在格点上,求:
