题目内容
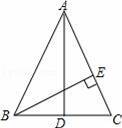
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.


【考点】等腰三角形的判定与性质;平行线的性质.
【分析】求出∠CAD=∠BAD=∠EDA,推出AE=DE,求出∠ABD=∠EDB,推出BE=DE,求出AE=BE,根据直角三角形斜边上中线性质求出即可.
【解答】解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE,
∵AD⊥DB,
∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,
∴DE=BE,
∵AB=5,
∴DE=BE=AE=
 AB=2.5.
AB=2.5.
【点评】本题考查了平行线的性质,等腰三角形的性质和判定,直角三角形斜边上中线性质的应用,关键是求出DE=BE=AE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 2+ 3x +4=0
2+ 3x +4=0





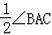
 ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC=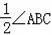

 ( )
( )
 )3÷(
)3÷( )2
)2 2,其中a=
2,其中a= ,b=
,b= .
.