题目内容
如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°.
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径长为1,求由弧BC、线段CD和BD所围成的阴影部分面积.(结果保留π和根号)

解:(1)直线CD与⊙O相切,
∵在⊙O中,∠COB=2∠CAB=2×30°=60°,
又∵OB=OC,
∴△OBC是正三角形,
∴∠OCB=60°,
又∵∠BCD=30°,
∴∠OCD=60°+30°=90°,
∴OC⊥CD,
又∵OC是半径,
∴直线CD与⊙O相切.
(2)由(1)得△OCD是Rt△,∠COB=60°,
∵OC=1,
∴CD= ,
,
∴S△COD= OC•CD=
OC•CD= ,
,
又∵S扇形OCB= ,
,
∴S阴影=S△COD﹣S扇形OCB= .
.

练习册系列答案
相关题目

 D.
D. 
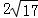 B.
B. 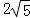 C.
C. 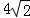 D. 7
D. 7 ,
, ,
, ,
, ,
, …,小亮猜想出第六个数字是
…,小亮猜想出第六个数字是 ,根据此规律,第n个数是
,根据此规律,第n个数是  B.
B.  C.
C.  D.
D. 
 的图象位于第二、四象限内,则m的取值范围是
的图象位于第二、四象限内,则m的取值范围是  B.
B.  C.
C.  D.
D. 
 ,其中
,其中 ,
, .
.