Question

已知在Rt△ABC中，∠C=90°，AC=3，BC=4．⊙O是Rt△ABC的外接圆，现小明同学随机的在⊙O及其内部区域做投针实验，则针投到Rt△ABC区域的概率是：________．

Answer 1

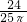
分析：根据几何概率，可得投到Rt△ABC区域的概率即Rt△ABC与其外接圆的面积比，由直角三角形的性质计算可得两者的面积，相比计算可得其概率．
解答：根据题意，易得S_△ABC=×3×4=6，
而⊙O是Rt△ABC的外接圆，则其AB为其直径，长为5，
其面积为π•（）²=，
根据几何概率，可得投到Rt△ABC区域的概率为=．
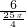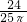故答案为．
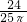点评：本题考查用面积法求概率，首先根据题意求得总面积与所求事件（A）表示区域的面积；然后事件（A）的面积在总面积中占的比例，这个比例即事件（A）发生的概率．