题目内容
 (1)已知在Rt△ABC中,∠C=90°,sinA=
(1)已知在Rt△ABC中,∠C=90°,sinA=| 5 | 13 |
(2)如图,小方在五月一日假期中到郊外放风筝,风筝飞到C 处时的线长为20米,此时小方正好站在A处,并测得∠CBD=60°,牵引底端B离地面1.5米,求此时风筝离地面的高度.
分析:(1)根据题意作出直角△ABC,然后根据sinA的值,设一条直角边BC为5,斜边AB为13,根据勾股定理求出另一条直角边AC的长度,然后根据三角函数的定义可求出tnaB.
(2)易得DE=AB,利用BC长和60°的正弦值即可求得CD长,加上DE长就是此时风筝离地面的高度.
(2)易得DE=AB,利用BC长和60°的正弦值即可求得CD长,加上DE长就是此时风筝离地面的高度.
解答:解:(1)如图所示:
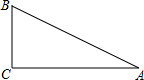
∵sinA=
∴设BC=5,AB=13,
则AC=12,
∴tanB=
=
.
(2)依题意得,∠CDB=∠BAE=∠ABD=∠AED=90°,
∴四边形ABDE是矩形,
∴DE=AB=1.5,
在Rt△BCD中,sin∠CBD=
,
又∵BC=20,∠CBD=60°,
∴CD=BC•sin60°=20×
=10
,
CE=10
+1.5≈19米,
答:此时风筝离地面的高度约为19米.

∵sinA=
| 5 |
| 13 |
∴设BC=5,AB=13,
则AC=12,
∴tanB=
| AC |
| BC |
| 12 |
| 5 |
(2)依题意得,∠CDB=∠BAE=∠ABD=∠AED=90°,
∴四边形ABDE是矩形,
∴DE=AB=1.5,
在Rt△BCD中,sin∠CBD=
| CD |
| BC |
又∵BC=20,∠CBD=60°,
∴CD=BC•sin60°=20×
| ||
| 2 |
| 3 |
CE=10
| 3 |
答:此时风筝离地面的高度约为19米.
点评:(1)本题考查了互余两角三角函数的关系,属于基础题,解题的关键是掌握三角函数的定义和勾股定理的运用.
(2)本题考查仰角的定义,能借助仰角构造直角三角形并解直角三角形是仰角问题常用的方法.
(2)本题考查仰角的定义,能借助仰角构造直角三角形并解直角三角形是仰角问题常用的方法.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 (2013•湖州)如图,已知在Rt△ACB中,∠C=90°,AB=13,AC=12,则cosB的值为
(2013•湖州)如图,已知在Rt△ACB中,∠C=90°,AB=13,AC=12,则cosB的值为 如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.
如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.