题目内容
8.直线y=x+1,y=-x+3和x轴围成的三角形的面积为( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
分析 联立两函数解析式可求得两直线的交点坐标,再求得两直线与x轴的交点坐标,再利用三角形面积可求得答案.
解答 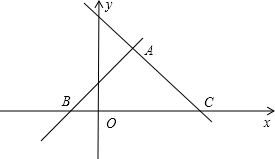 解:
解:
如图,设两直线交于点A,直线y=x+1与x轴交于点B,直线y=x+3与x轴交于点C,
联立两直线解析式可得$\left\{\begin{array}{l}{y=x+1}\\{y=-x+3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
∴A(1,2),
在y=x+1中,令y=0可得x=-1,在y=-x+3中,令y=0可得x=3,
∴B(-1,0),C(3,0),
∴BC=3-(-1)=4,
∴S△ABC=$\frac{1}{2}$×4×2=4,
即直线y=x+1,y=-x+3和x轴围成的三角形的面积为4,
故选C.
点评 本题主要考查一次函数图象上点的坐标特征,求得两直线的交点坐标是解题的关键,注意联立解析式求方程组的解是求函数图象交点坐标的常用方法.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
19.下列事件中,确定事件是( )
| A. | 当x是有理数时,x2≥0 | |
| B. | 某电影院今天的上座率超过80% | |
| C. | 射击运动员射击一次,命中8环 | |
| D. | 掷一枚普通的正方体骰子出现点数为6 |
16.若点A(a+3,a+1)在x轴上,则点a的值为( )
| A. | -1 | B. | -3 | C. | 0 | D. | 2 |
3.如果(x1,y1),(x2,y2)在直线y=3x-1上,且x1<x2,设M=$\frac{{y}_{1}+1}{{x}_{1}}$,N=$\frac{{y}_{2}+1}{{x}_{2}}$,那么( )
| A. | M>N | B. | M<N | C. | M=N | D. | M《N |
20.下列方程组中,与$\left\{\begin{array}{l}{x+2y=5}\\{2x+5y=7}\end{array}\right.$不同解的是( )
| A. | $\left\{\begin{array}{l}{x+2y=5}\\{3x+7y=12}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+3y=2}\\{2x+5y=7}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=5}\\{x+3y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3}\\{2x+5y=7}\end{array}\right.$ |