题目内容
如图，等腰Rt△ABC中，AB=AC，∠A=90°，点D为BC边的中点，E、F分别在AB、AC上，且ED⊥FD，EG⊥BC于G点，FH⊥BC于H点，下列结论：①DE=DF；②AE+AF=AB；③S四边形AEDF=
S△ABC；④EG+FH=BC．其中正确结论的序号是
- A.只有②③
- B.只有①②
- C.只有①②③
- D.①②③④
D
分析：考查直角三角形及等腰三角形的性质及判定问题，利用全等三角形判断线段相等，例如在①中，可求解Rt△EGD≌Rt△DHF，同样后面几问也都可用全等解答．
解答：
解：如图所示，
∵DE⊥DF，∴∠EDG+∠FDH=90°
∵∠EDG+∠GED=90°∴∠GED=∠FDH，
∴Rt△EGD≌Rt△DHF，∴DE=DF，①正确；
连接AD，由①得，DE=DF，
∵DC=AD，∠FDC=∠ADE，
∴可证△AED≌△CFD，
∴FC=AE，∴AE+AF=AB，②正确，
∵BE=AF，∠CAD=∠B=45°，AD为公共边，
∴△ADF≌△DEB，又△AED≌△CFD，∴③也正确，
④中由①得GD=FH，又∠B=45°
∴BG=EG，EG+FH=BC，④正确
∴①②③④都正确，故选D．
点评：熟练掌握等腰三角形及直角三角形的性质，能够通过全等求角相等，线段相等．
分析：考查直角三角形及等腰三角形的性质及判定问题，利用全等三角形判断线段相等，例如在①中，可求解Rt△EGD≌Rt△DHF，同样后面几问也都可用全等解答．
解答：
解：如图所示，∵DE⊥DF，∴∠EDG+∠FDH=90°
∵∠EDG+∠GED=90°∴∠GED=∠FDH，
∴Rt△EGD≌Rt△DHF，∴DE=DF，①正确；
连接AD，由①得，DE=DF，
∵DC=AD，∠FDC=∠ADE，
∴可证△AED≌△CFD，
∴FC=AE，∴AE+AF=AB，②正确，
∵BE=AF，∠CAD=∠B=45°，AD为公共边，
∴△ADF≌△DEB，又△AED≌△CFD，∴③也正确，
④中由①得GD=FH，又∠B=45°
∴BG=EG，EG+FH=
BC，④正确∴①②③④都正确，故选D．
点评：熟练掌握等腰三角形及直角三角形的性质，能够通过全等求角相等，线段相等．
练习册系列答案
相关题目
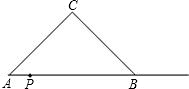PQ=AP，以PQ为一边向上作正方形PQMN，设正方形PQMN与Rt△ABC重叠部分的面积为S．
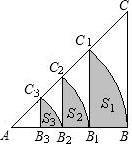如图，等腰Rt△ABC的直角边长为4，以A为圆心，直角边AB为半径作弧BC1，交斜边AC于点C1，C1B1⊥AB于点B1，设弧BC1，C1B1，B1B围成的阴影部分的面积为S1，然后以A为圆心，AB1为半径作弧B1C2，交斜边AC于点C2，C2B2⊥AB于点B2，设弧B1C2，C2B2，B2B1围成的阴影部分的面积为S2，按此规律继续作下去，得到的阴影部分的面积S3=
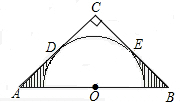如图，等腰Rt△ABC中斜边AB=4，O是AB的中点，以O为圆心的半圆分别与两腰相切于点D、E，图中阴影部分的面积是多少？请你把它求出来．（结果用π表示）
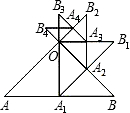已知：如图，等腰Rt△OAB的直角边OA的长为1，以AB边上的高OA1为直角边，按逆时针方向作等腰Rt△OA1B1，A1B1与OB相交于点A2．若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2，A2B2与OB1相交于点A3，按此作法进行下去，得到△OA3B3，△OA4B4，…，则△OA6B6的周长是
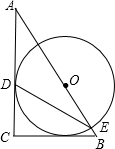如图，等腰Rt△ABC，AC=BC，以斜边AB中点O为圆心作⊙O与AC边相切于点D，交AB于点E，连接DE．