题目内容
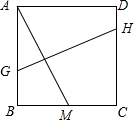 如图,边长为8的正方形ABCD中,M是BC上的一点,连结AM,作AM的垂直平分线GH交AB于G,交CD于H,若CM=2,则GH=________.
如图,边长为8的正方形ABCD中,M是BC上的一点,连结AM,作AM的垂直平分线GH交AB于G,交CD于H,若CM=2,则GH=________.
10
分析:先求出BM,再根据勾股定理列式求出AM,过点B作BN∥GH,可得四边形BNHG是平行四边形,根据平行四边形的对边相等可得BN=GH,再根据同角的余角相等求出∠BAM=∠CBN,然后利用“角边角”证明△ABM和△BCN全等,根据全等三角形对应边相等可得AM=BN,从而得解.
解答: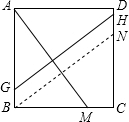 解:∵正方形ABCD的边长为8,CM=2,
解:∵正方形ABCD的边长为8,CM=2,
∴BM=8-2=6,
根据勾股定理,AM=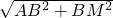 =
= =10,
=10,
如图,过点B作BN∥GH,则四边形BNHG是平行四边形,
∴BN=GH,
∵GH是AM的垂直平分线,
∴∠CBN+∠AMB=90°,
又∵∠BAM+∠AMB=90°,
∴∠BAM=∠CBN,
在△ABM和△BCN中,
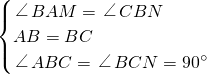 ,
,
∴△ABM≌△BCN(ASA),
∴AM=BN,
∴GH=AM=10.
故答案为:10.
点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的应用,作辅助线构造出全等三角形是解题的关键.
分析:先求出BM,再根据勾股定理列式求出AM,过点B作BN∥GH,可得四边形BNHG是平行四边形,根据平行四边形的对边相等可得BN=GH,再根据同角的余角相等求出∠BAM=∠CBN,然后利用“角边角”证明△ABM和△BCN全等,根据全等三角形对应边相等可得AM=BN,从而得解.
解答:
 解:∵正方形ABCD的边长为8,CM=2,
解:∵正方形ABCD的边长为8,CM=2,∴BM=8-2=6,
根据勾股定理,AM=
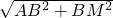 =
= =10,
=10,如图,过点B作BN∥GH,则四边形BNHG是平行四边形,
∴BN=GH,
∵GH是AM的垂直平分线,
∴∠CBN+∠AMB=90°,
又∵∠BAM+∠AMB=90°,
∴∠BAM=∠CBN,
在△ABM和△BCN中,
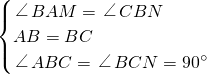 ,
,∴△ABM≌△BCN(ASA),
∴AM=BN,
∴GH=AM=10.
故答案为:10.
点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的应用,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目

 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P. 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
