题目内容
17．
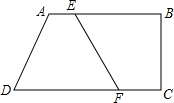如图，四边形ABCD中，AB∥CD，AB⊥BC，点E在AB边上从A向B以1cm/s的速度移动，同时点F在CD边上从C向D以2cm/s的速度移动，若AB=7cm，CD=9cm，则3秒时四边形ADFE是平行四边形．
分析 直接利用平行四边形的判定与性质得出AE=DF，进而得出答案．
解答 解：设t秒时四边形ADFE是平行四边形；
理由：当四边形ADFE是平行四边形，则AE=DF，
即t=9-2t，
解得：t=3，故3秒时四边形ADFE是平行四边形．
故答案为：3．
点评 此题主要考查了平行四边形的判定，得出AE=DF是解题关键．
练习册系列答案
相关题目
5．
不等式组的解集在数轴上表示如图，则该不等式组是（ ）
不等式组的解集在数轴上表示如图，则该不等式组是（ ）| A． | $\left\{\begin{array}{l}x≥-1\\ x≤2\end{array}\right.$ | B． | $\left\{\begin{array}{l}x＜-1\\ x≥2\end{array}\right.$ | C． | $\left\{\begin{array}{l}x＞-1\\ x＜2\end{array}\right.$ | D． | $\left\{\begin{array}{l}x＞-1\\ x≤2\end{array}\right.$ |
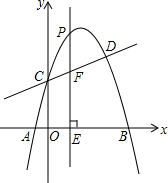如图，抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C，D两点，其中点C在y轴上，点D的坐标为（3，$\frac{7}{2}$）．点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F．
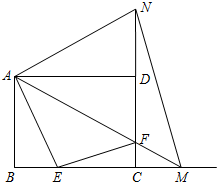如图，在矩形ABCD中，AB=9，AD=12．动点E从点B出发，沿线段BC（不包括端点B、C）以每秒2个单位长度的速度，匀速向点C运动；动点F从点C出发，沿线段CD（不包括端点C、D）以每秒1个单位长度的速度，匀速向点D运动；点E、F同时出发，同时停止．连接AF并延长交BC的延长线于点M，再把AM沿AD翻折交CD延长线于点N，连接MN．设运动时间为t秒．
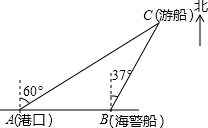一艘观光游船从港口A处以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号．一艘在港口正东方向B处的海警船接到求救信号，测得事故船在它的北偏东37°方向．
6．某车间56名工人，每人每天能生产螺栓16个或螺母24个，设有x名工人生产螺栓，有y名工人生产螺母，每天生产的螺栓和螺母按1：2配套，所列方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=56}\\{2×16x=24y}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=56}\\{2×24x=26y}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=56}\\{16x=24y}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=56}\\{24x=16y}\end{array}\right.$ |