Question

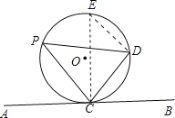
【题目】定义：弦切角：顶点在圆上，一边与圆相交，另一边和圆相切的角叫弦切角．

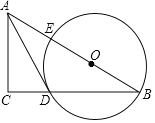
问题情景：已知如图所示，直线是的切线，切点为，为的一条弦，为弧所对的圆周角．

（1）猜想：弦切角与之间的关系．试用转化的思想：即连接并延长交于点，连接，来论证你的猜想．

（2）用自己的语言叙述你猜想得到的结论．

Answer 1

【答案】（1）（2）弦切角等于其两边所夹弧对的圆周角

【解析】

（1）连接CO并延长交圆于E，连接DE，根据直径所对的圆周角是直角，可以得到∠E+∠DCE=90°；再根据AB是切线可以得到∠DCE+DCB=90°，所以∠DCB=∠E，最后根据等弧所对的圆周角相等就可以的得到所要的结论．

（2）能说清弦切角与圆周角的关系即可．

（1）；

证明：∵是的直径，

∴；

又∵是的切线，

∴，

∴；

又∵，

∴．

（2）弦切角等于其两边所夹弧对的圆周角．

（或弦切角的度数等于其两边所夹弧度数的一半．）