题目内容
 在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=| k |
| x |
| 2 |
| 5 |
考点:反比例函数综合题
专题:
分析:由正切值可求得B点坐标,可得出A点的坐标,代入一次函数可求得一次函数的解析式,可求得C点坐标,可求得BC、OC、BO的长度,再设出M点的坐标,表示出OM,再由相似得到线段比例,可解得M点的坐标.
解答: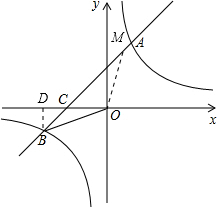 解:如图过点B作BD⊥x轴,交x轴于点D,
解:如图过点B作BD⊥x轴,交x轴于点D,
则tan∠BOC=
=
,
又因为B点坐标为(n,-2),
所以BD=2,OD=-n,
即
=
,
解得n=-5,
所以B点坐标为(-5,-2),
又因为A点也在反比例函数图象上,
所以2m=-5×(-2)=10,
解得m=5,
所以A点坐标为(2,5),
把A、B两点的坐标代入y=kx+b可得
解得
,即一次函数解析式为y=x+3,
所以可求得C点坐标为(-3,0),
因为M点在直线AB上,可设M点坐标为(x,x+3),
则OM=
,
在△OBC中,OB=
=
=
,
OC=3,OD=5,所以CD=5-3=2,且BD=2,所以可求得BC=2
,
要使△MBO∽△OBC,则有
=
,即
=
,
两边平方整理可得:16x2+48x-15=0,
解得x=±
-
,
当x=-
-
时,x+3=
-
,此时M点的坐标为(-
-
,
-
),
当x=
-
时,x+3=
+
,此时M点的坐标为(
-
,
+
).
 解:如图过点B作BD⊥x轴,交x轴于点D,
解:如图过点B作BD⊥x轴,交x轴于点D,则tan∠BOC=
| BD |
| OD |
| 2 |
| 5 |
又因为B点坐标为(n,-2),
所以BD=2,OD=-n,
即
| 2 |
| -n |
| 2 |
| 5 |
解得n=-5,
所以B点坐标为(-5,-2),
又因为A点也在反比例函数图象上,
所以2m=-5×(-2)=10,
解得m=5,
所以A点坐标为(2,5),
把A、B两点的坐标代入y=kx+b可得
|
解得
|
所以可求得C点坐标为(-3,0),
因为M点在直线AB上,可设M点坐标为(x,x+3),
则OM=
| x2+(x+3)2 |
在△OBC中,OB=
| OD2+BD2 |
| 52+22 |
| 29 |
OC=3,OD=5,所以CD=5-3=2,且BD=2,所以可求得BC=2
| 2 |
要使△MBO∽△OBC,则有
| OM |
| OC |
| BO |
| BC |
| ||
| 3 |
| ||
2
|
两边平方整理可得:16x2+48x-15=0,
解得x=±
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
当x=-
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |
当x=
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |
点评:本题主要考查一次函数和反比例函数及相似三角形的应用,求出一次函数的解析式,设出M点的坐标,利用相似的性质得出关于M坐标的方程是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
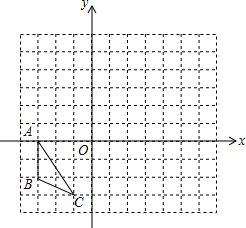 如图,在边长为1的正方网格内有一个三角形ABC.
如图,在边长为1的正方网格内有一个三角形ABC.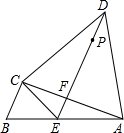 某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路DE直达该区域,小路DE和小路AC恰好互相垂直,垂足为F.
某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路DE直达该区域,小路DE和小路AC恰好互相垂直,垂足为F.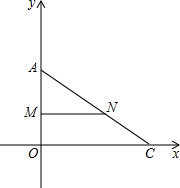 如图,平面直角坐标系中,点A,C两点分别在x轴和y轴上,点A的坐标点(0,6),点C的坐标(8,0),M、N分别为OA、AC的中点,动点P从O出发以每秒1个单位的速度沿折线OCNM运动,以P为圆心,以3为半径作⊙P,以N为圆心,以1为半径作⊙N.
如图,平面直角坐标系中,点A,C两点分别在x轴和y轴上,点A的坐标点(0,6),点C的坐标(8,0),M、N分别为OA、AC的中点,动点P从O出发以每秒1个单位的速度沿折线OCNM运动,以P为圆心,以3为半径作⊙P,以N为圆心,以1为半径作⊙N.