题目内容
(1)-3x2+22x-24=0
(2)(3x+5)2-4(3x+5)+3=0
(3)(3x+2)(x+3)=x+14
(4)6x2-x-12=0.
解:(1)∵方程-3x2+22x-24=0的二次项系数a=-3,一次项系数b=22,常数项c=-24,
∴x= =
=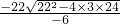 =
= ,
,
∴x1=6,x2= ;
;
(2)设3x+5=y,则原方程变为
y2-4y+3=0,
∴(y-1)(y-3)=0,
解得,y=1或y=3;
①当y=1时,3x+5=1,解得x=- ;
;
②当y=3时,3x+5=3,解得,x=- ;
;
∴原方程的解是x=- ,或x=-
,或x=- ;
;
(3)由原方程,得
(x+4)(3x-2)=0,
解得x=-4,或x= ;
;
(4)由原方程,得
(2x-3)(3x+4)=0,
解得,x= ,或x=-
,或x=- .
.
分析:(1)利用公式法解方程;
(2)利用换元法解方程;
(3)、(4)利用因式分解法解方程.
点评:本题考查了解一元二次方程--公式法、因式分解法、换元法.应根据方程的特点选择解方程的方法.
∴x=
 =
=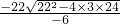 =
= ,
,∴x1=6,x2=
 ;
;(2)设3x+5=y,则原方程变为
y2-4y+3=0,
∴(y-1)(y-3)=0,
解得,y=1或y=3;
①当y=1时,3x+5=1,解得x=-
 ;
;②当y=3时,3x+5=3,解得,x=-
 ;
;∴原方程的解是x=-
 ,或x=-
,或x=- ;
;(3)由原方程,得
(x+4)(3x-2)=0,
解得x=-4,或x=
 ;
;(4)由原方程,得
(2x-3)(3x+4)=0,
解得,x=
 ,或x=-
,或x=- .
.分析:(1)利用公式法解方程;
(2)利用换元法解方程;
(3)、(4)利用因式分解法解方程.
点评:本题考查了解一元二次方程--公式法、因式分解法、换元法.应根据方程的特点选择解方程的方法.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目