题目内容
 如图,已知AB∥DC,AD∥BC,∠A是∠B的5倍,求∠C和∠D的度数.
如图,已知AB∥DC,AD∥BC,∠A是∠B的5倍,求∠C和∠D的度数.考点:平行线的性质
专题:
分析:根据平行线性质得出∠A+∠B=180°,∠C+∠B=180°,推出∠A=∠C,根据已知得出6∠B=180°,求出∠B=30°,进而求得∠C=∠A=150°根据平行线性质得出∠D+∠C=180°,即可求出∠D=30°.
解答:解:∵AB∥CD,AD∥BC,
∴∠A+∠B=180°,∠C+∠B=180°,
∴∠A=∠C,
∵∠A是∠B的5倍,
∴5∠B+∠B=180°,
即6∠B=180°,
∴∠B=30°,
∴∠A=150°,
∴∠C=150°,
∵AD∥BC,
∴∠D+∠C=180°,
∴∠D=180°-150°=30°.
∴∠A+∠B=180°,∠C+∠B=180°,
∴∠A=∠C,
∵∠A是∠B的5倍,
∴5∠B+∠B=180°,
即6∠B=180°,
∴∠B=30°,
∴∠A=150°,
∴∠C=150°,
∵AD∥BC,
∴∠D+∠C=180°,
∴∠D=180°-150°=30°.
点评:本题考查了平行线性质和互补的定义的应用,主要考查学生的推理能力和计算能力.

练习册系列答案
相关题目
在△ABC和△A′B′C′中,AB=9cm,BC=8cm,CA=5cm,A′B′=3cm,B′C′=
cm,C′A′=
cm,则( )
| 8 |
| 3 |
| 5 |
| 3 |
| A、∠B=∠A′ |
| B、∠A=∠C′ |
| C、∠A>∠B′ |
| D、∠C=∠B′ |
 如图所示,⊙O1与⊙O2外切于点P,并且⊙O与⊙O1、⊙O2分别内切于M、N,△O1O2O的周长为36cm,求⊙O的半径长.
如图所示,⊙O1与⊙O2外切于点P,并且⊙O与⊙O1、⊙O2分别内切于M、N,△O1O2O的周长为36cm,求⊙O的半径长.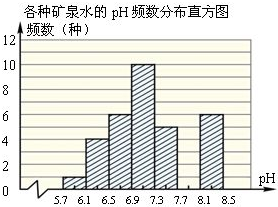 2008年 5月12日,我国四川省发生里氏8.0级地震,社会各界纷纷伸出援助之手捐钱捐物.根据国家质检总局的通知要求,对送往灾区食品、重要消费品必须进行检验检测,以确保运往灾区的食品等救灾物资的质量安全.如图是对某批数种矿泉水的抽查统计图,请观察图形,并回答下列问题:
2008年 5月12日,我国四川省发生里氏8.0级地震,社会各界纷纷伸出援助之手捐钱捐物.根据国家质检总局的通知要求,对送往灾区食品、重要消费品必须进行检验检测,以确保运往灾区的食品等救灾物资的质量安全.如图是对某批数种矿泉水的抽查统计图,请观察图形,并回答下列问题:
 如图,已知在⊙O中,直径AB=10cm,弦AC为6cm,∠ACB的平分线CD交⊙O于D,求BC、AD、BD的长.
如图,已知在⊙O中,直径AB=10cm,弦AC为6cm,∠ACB的平分线CD交⊙O于D,求BC、AD、BD的长.