题目内容
找规律:
(m-1)(m+1)=m2-1;
(m-1)(m2+m+1)=m3-1;
(m-1)(m3+m2+m+1)=m4-1;
(m-1)(m4+m3+m2+m+1)=m5-1;
(m-1)(m5+m4+m3+m2+m+1)=______-1;
…
( m-1)(mn-1+mn-2+…m2+m+1)=______-1;
(1)在上面空白处填空;
(2)根据你找的规律计算:2+22+23+…+298+299.
解:(1)(m-1)(m5+m4+m3+m2+m+1)=m6-1;
( m-1)(mn-1+mn-2+…m2+m+1)=mn-1;
故答案为m6,mn;
(2)2+22+23+…+298+299=1+1+22+23+…+298+299
=1+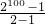
=1+(2100-1)
=2100.
分析:(1)等式左边为两个式子的积,一个为m-1,另一个是mn+mn-1+…m2+m+1,等式的右边是mn+1-1;
(2)把2+22+23+…+298+299变为1+1+22+23+…+298+299.
点评:通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.
本题的关键规律为等号前面m-1与mn+mn-1+…m2+m+1的积,等号右边是mn+1-1.
( m-1)(mn-1+mn-2+…m2+m+1)=mn-1;
故答案为m6,mn;
(2)2+22+23+…+298+299=1+1+22+23+…+298+299
=1+
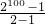
=1+(2100-1)
=2100.
分析:(1)等式左边为两个式子的积,一个为m-1,另一个是mn+mn-1+…m2+m+1,等式的右边是mn+1-1;
(2)把2+22+23+…+298+299变为1+1+22+23+…+298+299.
点评:通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.
本题的关键规律为等号前面m-1与mn+mn-1+…m2+m+1的积,等号右边是mn+1-1.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 表示3abc,方框
表示3abc,方框 表示-4xywz,求
表示-4xywz,求 ×
× .
. 找规律
找规律