题目内容
 如图,已知线段AB=8,延长BA至点C,使AC=
如图,已知线段AB=8,延长BA至点C,使AC=| 1 | 2 |
2
2
.分析:先根据AB=8,AC=
AB求出AC的长,故可得出线段BC的长,再根据D为线段BC的中点求出线段CD的长,根据AD=CD-AC即可得出结论.
| 1 |
| 2 |
解答:解:∵AB=8,AC=
AB,
∴AC=
×8=4,
∴BC=AC+AB=4+8=12,
∵D为线段BC的中点,
∴CD=
BC=
×12=6,
∴AD=CD-AC=6-4=2.
故答案为:2.
| 1 |
| 2 |
∴AC=
| 1 |
| 2 |
∴BC=AC+AB=4+8=12,
∵D为线段BC的中点,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=CD-AC=6-4=2.
故答案为:2.
点评:本题考查的是两点间的距离,在解答此类问题时要注意各线段之间的和、差及倍数关系.

练习册系列答案
相关题目
如图,已知线段AB=10cm,点C是AB上任一点,点M、N分别是AC和CB的中点,则MN的长度为( )


| A、6cm | B、5cm | C、4cm | D、3cm |
 如图,已知线段AB,延长AB至C,使得BC=
如图,已知线段AB,延长AB至C,使得BC=| 1 |
| 2 |
| A、4cm | B、8cm |
| C、10cm | D、12cm |


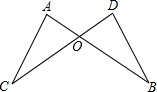 如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.
如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.