题目内容
如图在Rt△ABC中,∠A=90°,AB=10,AC=5,若动点P从点B出发,沿线段BA运动到A点为止,运动为 每秒2个单位长度.过点P作PM∥BC,交AC于点M,设动点P运动时间为x秒,AM的长为y.
每秒2个单位长度.过点P作PM∥BC,交AC于点M,设动点P运动时间为x秒,AM的长为y.(1)求出y关于x的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,△BPM的面积S有最大值,最大值是多少?
分析:(1)由PN、BC平行易得△APM∽△ABC,即得到
=
,由题意代入各线段的值,即可得解.
(2)由三角形面积公式得,△BPM的面积S=
BP•AM,据(1)中条件可得到一个关于x的二次函数式,求x的最大值即得面积的最大值.
| AP |
| AB |
| AM |
| AC |
(2)由三角形面积公式得,△BPM的面积S=
| 1 |
| 2 |
解答:解:(1)∵PM∥BC
∴△APM∽△ABC,
∴
=
,
又∵AP=10-2x,AB=10,AM=y,AC=5,
∴y=-x+5;
∵x≥0,y≥0,
∴自变量x的取值范围为0≤x≤5.
(2)S=
BP•AM
=
•2x(-x+5)
=-x2+5x
=-(x-
)2+
.
∴当x=
时,S有最大值,最大值为
.
∴△APM∽△ABC,
∴
| AP |
| AB |
| AM |
| AC |
又∵AP=10-2x,AB=10,AM=y,AC=5,
∴y=-x+5;
∵x≥0,y≥0,
∴自变量x的取值范围为0≤x≤5.
(2)S=
| 1 |
| 2 |
=
| 1 |
| 2 |
=-x2+5x
=-(x-
| 5 |
| 2 |
| 25 |
| 4 |
∴当x=
| 5 |
| 2 |
| 25 |
| 4 |
点评:本题主要考查相似三角形的判定、三角形的面积及涉及到二次函数的最值问题,找到等量比是解题的关键.

练习册系列答案
相关题目
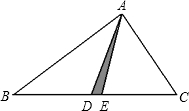 如图在Rt△ABC中,∠BAC=90°,AB=5,AC=4,AD、AE分别是△ABC的中线和角平分线,则△ADE的面积为
如图在Rt△ABC中,∠BAC=90°,AB=5,AC=4,AD、AE分别是△ABC的中线和角平分线,则△ADE的面积为 如图在Rt△ABC中,∠ACB=90°,sinA=
如图在Rt△ABC中,∠ACB=90°,sinA=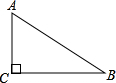 如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB=
如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB=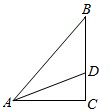 如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是
如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是 (1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=
(1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=