题目内容
如图,在平面直角坐标系中,O为坐标原点,直线y=﹣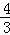 x+4与x轴交于点B,与y轴交于点A,点C在x轴的负半轴上,并且OC=OB,一动点P在射线AB上运动,连结CP交y轴于点D,连结BD.过B,P,D三点作圆,交y轴与点E,过点E作EF∥x轴,交圆于点F,连结BF,DF.
x+4与x轴交于点B,与y轴交于点A,点C在x轴的负半轴上,并且OC=OB,一动点P在射线AB上运动,连结CP交y轴于点D,连结BD.过B,P,D三点作圆,交y轴与点E,过点E作EF∥x轴,交圆于点F,连结BF,DF.
(1)求点C的坐标.
(2)若动点P在线段AB上运动,
①求证∠EDB=∠ADP;
②设AP=n,CP=m,求当n为何值时,m的值最小?最小值是多少?
(3)试探究:点P在运动的过程中,当△BDF为直角三角形,并且两条直角边之比为2:1时,请直接写出OD的长 .

解:(1)令x=0,则y=4,
∴A(0,4),
令y=0,则﹣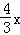 +4=0,x=3,
+4=0,x=3,
∴B(3,0),
又∵OC=OB=3,且点C在负半轴上,
∴C点的坐标为(﹣3,0);
(2)①在△DOC与△DOB中,
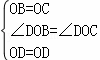 ,
,
∴△DOC≌△DOB(SAS),
∴∠CDO=∠BDO,
又∵∠CDO=∠ADP,
∴∠BDO=ADP,
即∠BDE=∠ADP;
②要使CP的长最短,则需CP⊥AB,
∴∠CPB=90°,
∵∠CBP=∠ABO,
∠AOB=∠CPB=90°,
∴Rt△BPC∽Rt△BOA,
∴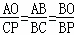 ,
,
∴ =
=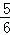 =
=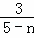 ,
,
解得:n=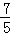 ,m=
,m=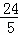 ,
,
即n=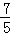 时,m有最小值,最小值为
时,m有最小值,最小值为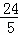 ;
;
(3)①当BD:BF=2:1时,
如图1,过点F作FH⊥OB于点H,
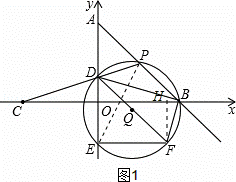
∵∠DBO+∠OBF=90°,∠OBF+∠BFH=90°,
∴∠DBO=∠BFH,
又∵∠DOB=∠BHF=90°,
∴△BOD∽△FHB,
∴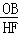 =
=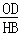 =
=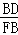 =2,
=2,
∴FH=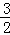 ,OD=2BH,
,OD=2BH,
∵∠FHO=∠EOH=∠OEF=90°,
∴四边形OEFH是矩形,
连结PE,
∵∠ADP是△DPE的一个外角,
∴∠ADP=∠DEP+∠DPE,
∵∠BDE是△ABD的一个外角,
∴∠BDE=∠ABD+∠OAB,
∵∠ADP=∠BDE,∠DEP=∠ABD,
∴∠DPE=∠OAB,
∴∠DFE=∠OAB,
∴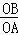 =
=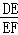 ,即
,即 =
=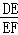 ,
,
∴DE= EF,
EF,
∴OD+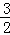 =
= ×(3﹣
×(3﹣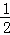 OD),解得OD=
OD),解得OD= ;
;
②当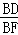 =
=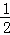 时,
时,
如图2,连结EB,过点F作FG⊥OB于点G,
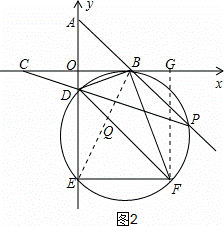
同理可得DE=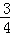 EF,
EF,
同理可得:△BOD∽△FGB,
∴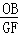 =
=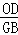 =
=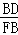 =
=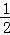 ,
,
∴FG=6,OD=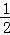 BG,
BG,
∵∠FGO=∠GOE=∠OEF=90°,
∴四边形OEFG是矩形,
6﹣OD=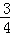 ×(3+2OD),解得OD=
×(3+2OD),解得OD=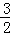 .
.
综上所述:当△BDF为直角三角形,并且两条直角边之比为2:1时,OD的长为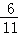 或
或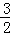 .
.
故答案为: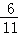 或
或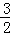 .
.

 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
 B.
B.  C.
C.  D.
D. 

 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )