题目内容
如图，在△AMC中，已知BD∥CM，AC+AB=14，且AM：AD=4：3，求AB的长．
解：∵BD∥CM，
∴AC：AB=AM：AD=4：3，
∵AC+AB=14，
∴AC=
×14=8，AB=
×14=6，
∴AB的长为6．
分析：由BD∥CM，根据平行线分线段成比例定理，即可得AC：AB=AM：AD=4：3，又由AC+AB=14，即可求得AB的长．
点评：此题考查了平行线分线段成比例定理．此题比较简单，解题的关键是注意数形结合思想的应用．
∴AC：AB=AM：AD=4：3，
∵AC+AB=14，
∴AC=
×14=8，AB=×14=6，∴AB的长为6．
分析：由BD∥CM，根据平行线分线段成比例定理，即可得AC：AB=AM：AD=4：3，又由AC+AB=14，即可求得AB的长．
点评：此题考查了平行线分线段成比例定理．此题比较简单，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
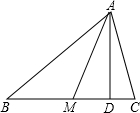如图，在△ABC中，AM是中线，AD是高线．
如图，在△AMC中，已知BD∥CM，AC+AB=14，且AM：AD=4：3，求AB的长．
