题目内容
12.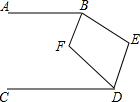 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°.
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°.(1)直接写出:∠ABE+∠CDE=220°;
(2)求∠BFD的度数.
分析 (1)过点E作EH∥AB,然后由AB∥CD,可得AB∥EH∥CD,然后根据两直线平行内错角相等可得∠ABE=∠BEH,∠CDE=∠DEH,然后根据周角的定义可求∠ABE+∠CDE的度数;
(2)先根据角平分线的定义求出∠EBF+∠EDF的度数,然后根据四边形的内角和定理即可求∠BFD的度数.
解答 解:(1)过点E作EH∥AB,如图所示,
∵AB∥CD,
∴AB∥EH∥CD,
∴∠ABE=∠BEH,∠CDE=∠DEH,
∵∠BEH+∠DEH++∠BED=360°,∠BED=140°,
∴∠BEH+∠DEH=220°,
∴∠ABE+∠CDE=220°,
故答案为:220;
(2)∵∠ABE和∠CDE的平分线相交于F,
∴∠EBF+∠EDF=$\frac{1}{2}$(∠ABE+∠CDE)=110°,
∵∠BFD+∠BED+∠EBF+∠EDF=360°,
∴∠BFD=110°.
点评 此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.另外过点E作EH∥AB,也是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.如图1,在矩形ABCD中,动点P从点B出发,沿BC-CD-DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则y的最大值是( )
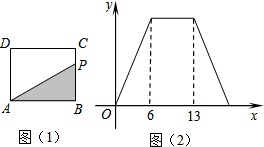

| A. | 78 | B. | 30 | C. | 21 | D. | 12 |
17.下列计算错误的是( )
| A. | a•a5÷a4=a2 | B. | a3÷a=a3 | C. | a2÷(-a)2=1 | D. | a3÷a•a2=a4 |
1.具备下列条件的两个三角形可以判定它们全等的是( )
| A. | 一边和这边上的高对应相等 | |
| B. | 两边和第三边上的高对应相等 | |
| C. | 两边和其中一边的对角对应相等 | |
| D. | 两个直角三角形中的一条直角边、斜边对应相等 |
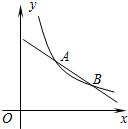 如图,反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的图象交于点A(m,m+1)、B(m+3,m-1).
如图,反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的图象交于点A(m,m+1)、B(m+3,m-1). 如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,那么BA是否平分∠EBF,试说明理由.
如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,那么BA是否平分∠EBF,试说明理由.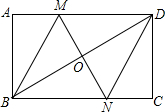 已知:如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
已知:如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.