题目内容
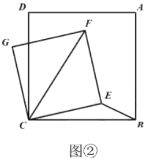
【题目】如图,以点O为圆心,OE为半径作优弧EF,连接OE,OF,且OE=3,∠EOF=120°,在弧EF上任意取点A,B(点B在点A的顺时针方向)且使AB=2,以AB为边向弧内作正三角形ABC.
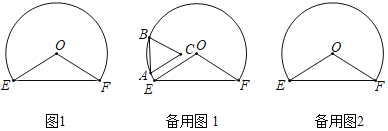
(1)发现:不论点A在弧上什么位置,点C与点O的距离不变,点C与点O的距离是 ;点C到直线EF的最大距离是 .
(2)思考:当点B在直线OE上时,求点C到OE的距离,在备用图1中画出示意图,并写出计算过程.
(3)探究:当BC与OE垂直或平行时,直接写出点C到OE的距离.
【答案】(1)![]() ;
;![]() ;(2)示意图见解析,点C到OE的距离为
;(2)示意图见解析,点C到OE的距离为![]() ;(3)当BC与OE垂直或平行时,点C到OE的距离为
;(3)当BC与OE垂直或平行时,点C到OE的距离为![]() 或
或![]() .
.
【解析】
(1)连接OB,OA,再连接OC并延长交AB于点G, 易知GO为线段AB的垂直平分线,通过勾股定理分别计算CG,GO的长,得到CO=GO-CG为定值即可;延长CO交EF于点H,当CO⊥EF时,点C到直线EF的距离最大,最大距离为CH的长,且CH=CO+OH,只需计算OH即可求出最大距离CH的长;
(2)过点C作OE的垂线,垂足为M,易证△OCM∽△OBG,得到![]() ,从而得到CM的长,即为点C到OE的距离;
,从而得到CM的长,即为点C到OE的距离;
(3)因为OC长不变,已求得,当BC与OE垂直或平行时,过点C作OE的垂线,利用OC不变,通过解相应的直角三角形,得到点C到OE的距离.
解:(1)如图1,连接OA、OB、OC,延长OC交AB于点G,
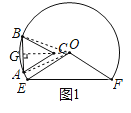
在正三角形ABC中,AB=BC=AC=2,
∵OA=OB,AC=BC,
∴OC垂直平分AB,
∴AG=![]() AB=1,
AB=1,
∴在Rt△AGC中,由勾股定理得:CG=![]() ,
,
在Rt△AGO中,由勾股定理得:OG=![]() ,
,
∴OC=![]() ;
;
如图2,延长CO交EF于点H,
当CO⊥EF时,点C到直线EF的距离最大,最大距离为CH的长,
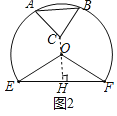
∵OE=OF,CO⊥EF,
∴CO平分∠EOF,
∵∠EOF=120°,
∴∠EOH=![]() ∠EOF=60°,
∠EOF=60°,
在Rt△EOH中,cos∠EOH=![]() ,
,
∴cos60°=![]() =
=![]() ,
,
∴OH=![]() ,
,
∴CH=CO+OH=![]() ,
,
∴点C到直线EF的最大距离是![]() .
.
故答案为:![]() ;
;![]() .
.
(2)如图3,当点B在直线OE上时,过点C作OE的垂线,垂足为M
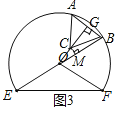
由OA=OB,CA=CB可知,
点O,C都在线段AB的垂直平分线上,
过点C作AB的垂线,垂足为G,
则G为AB中点,直线CG过点O.
∴由∠COM=∠BOG,∠CMO=∠BGO
∴△OCM∽△OBG,
∴![]() ,
,
∴![]() ,
,
∴CM=![]() ,
,
∴点C到OE的距离为![]() .
.
(3)如图4,当BC⊥OE时,设垂足为点M,
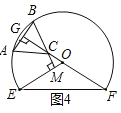
∵∠EOF=120°,
∴∠COM=180°﹣120°=60°,
∴在Rt△COM中,sin∠COM=![]() ,
,
∴sin60°=![]() =
=![]() ,
,
∴CM=![]() CO=
CO=![]() (
(![]() )=
)=![]() ;
;
如图5,当BC∥OE时,过点C作CN⊥OE,垂足为N,
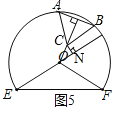
∵BC∥OE,
∴∠CON=∠GCB=30°,
∴在Rt△CON中,sin∠CON=![]() ,
,
∴sin30°=![]() =
=![]() ,
,
∴CN=![]() CO=
CO=![]() (
(![]() )=
)=![]() ;
;
综上所述,当BC与OE垂直或平行时,点C到OE的距离为![]() 或
或![]() .
.

 全优点练单元计划系列答案
全优点练单元计划系列答案