Question

5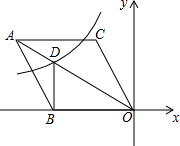．如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC=60°，顶点C的坐标为（m，3$\sqrt{3}$），x反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于点D，连接BD，当BD⊥x轴时，k的值是-12$\sqrt{3}$．

Answer 1

分析 延长AC交y轴于E，如图，根据菱形的性质得AC∥OB，则AE⊥y轴，再由∠BOC=60°得到∠COE=30°，则根据含30度的直角三角形三边的关系得到CE=$\frac{\sqrt{3}}{3}$OE=3，OC=2CE=6，接着根据菱形的性质得OB=OC=6，∠BOA=30°，于是在Rt△BDO中可计算出BD=$\frac{\sqrt{3}}{3}$OB=2$\sqrt{3}$，所以D点坐标为（-6，2$\sqrt{3}$），然后利用反比例函数图象上点的坐标特征可求出k的值．

解答 解：延长AC交y轴于E，如图，
∵菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，
∴AC∥OB，
∴AE⊥y轴，
∵∠BOC=60°，
∴∠COE=30°，
而顶点C的坐标为（m，3$\sqrt{3}$），
∴OE=3$\sqrt{3}$，
∴CE=$\frac{\sqrt{3}}{3}$OE=3，
∴OC=2CE=6，
∵四边形ABOC为菱形，
∴OB=OC=6，∠BOA=30°，
在Rt△BDO中，
∵BD=$\frac{\sqrt{3}}{3}$OB=2$\sqrt{3}$，
∴D点坐标为（-6，2$\sqrt{3}$），
∵反比例函数y=$\frac{k}{x}$的图象经过点D，
∴k=-6×2$\sqrt{3}$=-12$\sqrt{3}$．
故答案为-12$\sqrt{3}$．

点评 本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．也考查了含30度的直角三角形三边的关系．