题目内容
14.设直线x=1是函数y=ax2+bx+c(a,b,c是实数,且a<0)的图象的对称轴,( )| A. | 若m>1,则(m-1)a+b>0 | B. | 若m>1,则(m-1)a+b<0 | ||
| C. | 若m<1,则(m+1)a+b>0 | D. | 若m<1,则(m+1)a+b<0 |
分析 根据对称轴,可得b=-2a,根据有理数的乘法,可得答案.
解答 解:由对称轴,得
b=-2a.
(m+1)a+b=ma+a-2a=(m-1)a,
当m>1时,(m-1)a<0,(m-1)a+b与0无法判断.
当m<1时,(m-1)a>0,(m-1)a+b(m-1)a-2a=(m-1)a>0.
故选:C.
点评 本题考查了二次函数图象与系数的关系,利用对称轴得出b=-2a是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.下列运算中,结果正确的是( )
| A. | (a3)2=a6 | B. | (ab)3=a3b | C. | a•a3=a3 | D. | a8÷a4=a2 |
5.下列计算结果正确的是( )
| A. | 8a-a=8 | B. | a3•a2=a6 | C. | (-a)4=a4 | D. | (a-b)2=a2-b2 |
2.中华国山-五岳独尊的泰山,海拔1545米,1545用科学记数法表示为( )
| A. | 1.545×103 | B. | 1.545×104 | C. | 1.545×10-3 | D. | 1.545×10-4 |
9.在国家“一带一路”战略下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途经城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示应为( )
| A. | 0.13×105 | B. | 1.3×104 | C. | 1.3×105 | D. | 13×103 |
6.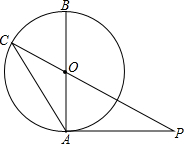 如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
 如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )| A. | $5\sqrt{3}$ | B. | $5\sqrt{2}$ | C. | 5 | D. | $\frac{5}{2}$ |
4.实数2,$\sqrt{2}$,$\frac{1}{2}$,0中,无理数是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | 0 |



