题目内容
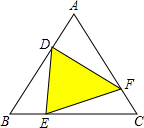如图，三角形ABC中，点D在AB上，BD=2AD，点E在BC上，BC=4BE，点F在AC上，AC=5CF，已知阴影三角形DEF的面积是25，那么三角形ABC的面积是________．
60
分析：作AG⊥BC，DH⊥BC，如图，根据平行线的性质，可得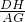
=
=
，根据三角形的面积计算公式，可得S△BED：S△ABC=
，同理，可得S△CFE：S△ABC=
，S△AFD：S△ABC=
，所以，可得三角形DEF占的面积比，即可得出三角形ABC的面积．
解答：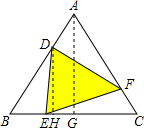
解：如图，作AG⊥BC，DH⊥BC，
∵BD=2AD，
∴==，
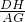∵S△BED=
BE×DH，S△ABC=BC×AG，
∵BC=4BE，
∴S△BED：S△ABC=，
同理，可得S△CFE：S△ABC=，
S△AFD：S△ABC=，
∴S△ABC=25÷（1---）=60．
故答案为：60．
点评：本题主要考查了三角形的面积和相似比，关键是求出三个小三角形所占的面积比，体现了转化思想．
分析：作AG⊥BC，DH⊥BC，如图，根据平行线的性质，可得
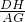==，根据三角形的面积计算公式，可得S△BED：S△ABC=，同理，可得S△CFE：S△ABC=，S△AFD：S△ABC=，所以，可得三角形DEF占的面积比，即可得出三角形ABC的面积．解答：
解：如图，作AG⊥BC，DH⊥BC，∵BD=2AD，
∴
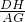==，∵S△BED=
BE×DH，S△ABC=BC×AG，∵BC=4BE，
∴S△BED：S△ABC=
，同理，可得S△CFE：S△ABC=
，S△AFD：S△ABC=
，∴S△ABC=25÷（1-
--）=60．故答案为：60．
点评：本题主要考查了三角形的面积和相似比，关键是求出三个小三角形所占的面积比，体现了转化思想．
练习册系列答案
活力课时同步练习册系列答案
相关题目
16、如图，三角形ABC中，∠C=90°，它的三边AB、AC、BC中，
15、如图，三角形ABC中任意一点P（x，y），经过平移后对应的点Q（x+5，y+3），将三角形ABC作同样的平移到三角形A1B1C1．
已知：如图等腰三角形ABC中，AB=AC，BD平分∠ABC交AC于D，若∠BDC=78°，求∠C的度数？
如图，三角形ABC中，顶点B的位置表示为（1，2），点A的位置表示为（2，4）．则点C表示位置为
画图并计算，在如图的三角形ABC中：