题目内容
 已知:如图等腰三角形ABC中,AB=AC,BD平分∠ABC交AC于D,若∠BDC=78°,求∠C的度数?
已知:如图等腰三角形ABC中,AB=AC,BD平分∠ABC交AC于D,若∠BDC=78°,求∠C的度数?
分析:首先根据AB=AC可得到∠ABC=∠ACB,再根据角平分线的性质可得∠ABD=∠DBC=
∠ABC=
∠C,设出∠C=x°,可根据三角形内角和定理求出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵AB=AC,
∴∠ABC=∠ACB,
∵BD平分∠B交AC于点D,
∴∠ABD=∠DBC=
∠ABC=
∠C,
设∠C=x°,则∠DBC=
x°,
∵∠BDC=78°,
∴x+
x+78=180,
解得:x=68,
∴∠C的度数是68°.
∴∠ABC=∠ACB,
∵BD平分∠B交AC于点D,
∴∠ABD=∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
设∠C=x°,则∠DBC=
| 1 |
| 2 |
∵∠BDC=78°,
∴x+
| 1 |
| 2 |
解得:x=68,
∴∠C的度数是68°.
点评:此题主要考查了等腰三角形的性质,以及三角形内角和定理,关键是根据条件理清角之间的关系,然后再利用方程思想解决即可.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
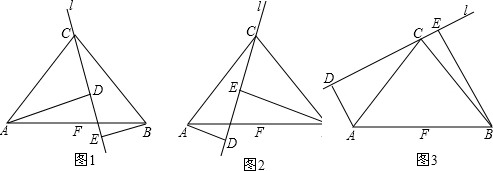
 24、先阅读下面的材料,然后解答问题:
24、先阅读下面的材料,然后解答问题:
 已知:如图等腰三角形ABC中,AB=AC,BD平分∠ABC交AC于D,若∠BDC=78°,求∠C的度数?
已知:如图等腰三角形ABC中,AB=AC,BD平分∠ABC交AC于D,若∠BDC=78°,求∠C的度数?