题目内容
从长度分别为2,3,6,7的四条线段中随机取三条,能构成三角形的概率是 .
考点:列表法与树状图法,三角形三边关系
专题:计算题
分析:利用列举法展示所有所有等可能的结果,再根据三角形三边的关系得到2、6、7和3、6、7能构成三角形,然后根据概率公式求解.
解答:解:从长度分别为2,3,6,7的四条线段中随机取三条,所有等可能的结果为:2、3、6;2、3、7;2、6、7;3、6、7,其中能构成三角形有2、6、7和3、6、7两种结果,
所以能构成三角形的概率=
=
.
故答案为
.
所以能构成三角形的概率=
| 2 |
| 4 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求解.也考查了三角形三边的关系.

练习册系列答案
相关题目
下列各式正确的是( )
A、
| ||||
B、-
| ||||
| C、-0.1>-(-0.01) | ||||
| D、-π<-3.14 |
 如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为 在△ABC中,∠B=63°,∠C=46°,AD和AE分别是它的高和角平分线,求∠DAE的度数.
在△ABC中,∠B=63°,∠C=46°,AD和AE分别是它的高和角平分线,求∠DAE的度数.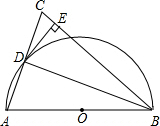 如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D.连结DB,过点D 作DE⊥BC,垂足为点E.
如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D.连结DB,过点D 作DE⊥BC,垂足为点E.