题目内容
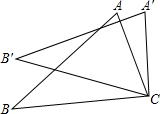如图，将△ABC绕点C顺时针旋转35°，得△A′B′C，若AC⊥A′B′，则∠BAC=（ ）| A、65° | B、75° |
| C、55° | D、35° |
考点：旋转的性质
专题：计算题
分析：根据旋转的性质得∠ACA′=35°，∠A=∠A′，再利用垂直的定义得到∠A′+∠ACA′=90°，则可计算出∠A′=55°，所以∠A=55°．
解答：解：∵△ABC绕点C顺时针旋转35°，得△A′B′C，
∴∠ACA′=35°，∠A=∠A′，
∵AC⊥A′B′，
∴∠A′+∠ACA′=90°，
∴∠A′=90°-35°=55°，
∴∠A=55°．
故选C．
∴∠ACA′=35°，∠A=∠A′，
∵AC⊥A′B′，
∴∠A′+∠ACA′=90°，
∴∠A′=90°-35°=55°，
∴∠A=55°．
故选C．
点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
练习册系列答案
相关题目
已知线段AB=8cm，在直线AB上有一点C，且BC=4cm，点M是线段AC的中点，则线段AM的长为（ ）
| A、2cm |
| B、4cm |
| C、2cm或6cm |
| D、4cm或6cm |
如图，BE是⊙O的直径，点A，C，D，F都在⊙O上，
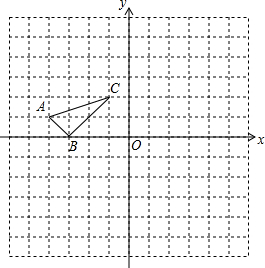每个小正方形边长都为1个单位长度．
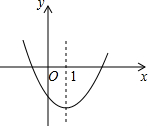二次函数y=ax2+bx+c图象如图，下列正确的个数为（ ）