Question

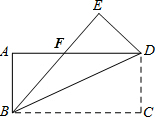如图，把一张长方形纸片ABCD沿对角线BD折叠，使C点落在E处，BE与AD相交于点F，下列结论：
①BD=AD²+AB²；②△ABF≌△EDF；③

DE

AB

=

EF

AF

；④AD=BD•cos45°．
其中正确的一组是（　　）

• A、①②
• B、②③
• C、①④
• D、③④

Answer 1

分析：①直接根据勾股定理即可判定是否正确；
②利用折叠可以得到全等条件证明△ABF≌△EDF；
③利用全等三角形的性质即可解决问题；
④在Rt△ABD中利用三角函数的定义即可判定是否正确．

解答：解：①∵△ABD为直角三角形，∴BD²=AD²+AB²，不是BD=AD²+AB²，故说法错误；
②根据折叠可知：DE=CD=AB，∠A=∠E，∠AFB=∠EFD，∴△ABF≌△EDF，故说法正确；
③根据②可以得到△ABF∽△EDF，∴

DE

AB

=

EF

AF

，故说法正确；
④在Rt△ABD中，∠ADB≠45°，∴AD≠BD•cos45°，故说法错误．
所以正确的是②③．
故选B．

点评：此题主要考查了折叠问题，也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义，它们的综合性比较强，对于学生的综合能力要求比较高，平时加强训练．