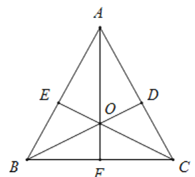
题目内容
【题目】![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 上的两动点,
上的两动点,![]() 从点
从点![]() 开始以
开始以![]() 的速度向点
的速度向点![]() 运动,
运动,![]() 从点
从点![]() 开始以
开始以![]() 的速度向点
的速度向点![]() 运动,当一点到达终点时,
运动,当一点到达终点时,![]() 、
、![]() 两点就同时停止运动.设运动时间为
两点就同时停止运动.设运动时间为![]() .
.

(1)用![]() 的代数式分别表示
的代数式分别表示![]() 和
和![]() 的长;
的长;
(2)设![]() 的面积为
的面积为![]() ,
,
①求![]() 的面积
的面积![]() 与
与![]() 的关系式;
的关系式;
②当![]() 时,
时,![]() 的面积
的面积![]() 是多少?
是多少?
(3)当![]() 为多少秒时,以点
为多少秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
【答案】![]() ,
,![]() ;
;![]() ①
①![]() ,②
,②![]() ;
;![]() 当
当![]() 为
为![]() 秒或
秒或![]() 时,以点
时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
【解析】
(1)用t的代数式分别表示AQ=2t,AP=6-t;
(2)设△APQ的面积为S,
①根据三角形的面积公式可知![]() ,即S=6t-t2;
,即S=6t-t2;
②当t=2s时,代入三角形的面积公式即可求值.
(3)①当当![]() 时
时![]() ,则有t=2.4(s);
,则有t=2.4(s);
②当![]() 时
时![]() ,则有
,则有![]() ;
;
![]() 用
用![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() ;
;
![]() 设
设![]() 的面积为
的面积为![]() ,
,
①![]() 的面积
的面积![]() 与
与![]() 的关系式为:
的关系式为:![]() ,即
,即![]() ,
,
②当![]() 时,
时,![]() 的面积
的面积![]() ;
;
![]() 当
当![]() 为多少秒时,以点
为多少秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
①当![]() 时
时![]() ,∴
,∴![]() ;
;
②当![]() 时
时![]() ,∴
,∴![]() ;
;
综上所述,当![]() 为
为![]() 秒或
秒或![]() 时,
时,
以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】甲、乙两名同学的家与学校的距离均为![]() .甲同学先步行
.甲同学先步行![]() ,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的
,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的![]() 倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到
倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到![]() .
.
(1)解:设乙同学骑自行车的速度为![]() .完成表格:
.完成表格:
乙同学 | 甲同学 | ||
骑自行车 | 步行 | 乘公交车 | |
路程 |
|
| |
时间 |
| ||
(2)求乙同学骑自行车的速度.
(3)当甲同学到达学校时,乙同学离学校还有多少米?
【题目】今年春北方严重干旱,某社区人畜饮水紧张,每天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨,从两水厂运水到社区供水点的路程和运费如下表:
到社区供水点的路程(千米) | 运费(元/吨·千米) | |
甲厂 | 20 | 12 |
乙厂 | 14 | 15 |
【1】若某天调运水的总运费为26700元,则从甲、乙两水厂各调运多少吨饮用水?
【2】设从甲厂调运饮用水![]() 吨,总运费为W元,试写出W关于与
吨,总运费为W元,试写出W关于与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?