题目内容
【题目】如图,![]() 中,
中,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() 的面积为54,则线段
的面积为54,则线段![]() 的长为__________.
的长为__________.
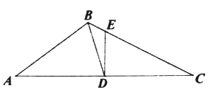
【答案】6![]()
【解析】
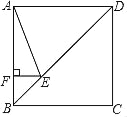
过C点作CN⊥AB的延长线于N,过B点作BM⊥AC于M,根据DE垂直平分AC,从而证出![]() ,再根据
,再根据![]() ,从而证出
,从而证出![]() ,证出MC=NC,设AB=x,DM=y,则CN=x+y,然后根据
,证出MC=NC,设AB=x,DM=y,则CN=x+y,然后根据![]() ,得到AB:AC=AM:AN,继而得出AN=2(x-y),在Rt
,得到AB:AC=AM:AN,继而得出AN=2(x-y),在Rt![]() 中,根据勾股定理得出x和y的关系,再根据
中,根据勾股定理得出x和y的关系,再根据![]() 的面积为54,所以有
的面积为54,所以有![]() 的面积也为54,所以
的面积也为54,所以![]() ,从而求出x、y的值,再根据BD2=x2-(x-y)2+y2,即可求出答案.
,从而求出x、y的值,再根据BD2=x2-(x-y)2+y2,即可求出答案.
过C点作CN⊥AB的延长线于N,过B点作BM⊥AC于M.

∵DE垂直平分AC
∴BM//DE
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵BM⊥AC,CN⊥AB
∴MC=CN
设AB=x,DM=y
∵AB=AD, DE垂直平分AC
∴AD=CD=x,CN=x+y
∵![]() 的面积为54
的面积为54
∴![]() 的面积也为54
的面积也为54
∴![]()
∵![]() ,
,![]()
∴![]()
∴AB:AC=AM:AN=1: 2
∴AN=2AM=2(x-y)
在Rt![]() 中,根据勾股定理可得,(x+y)2+[2(x+y)]2=(2x)2
中,根据勾股定理可得,(x+y)2+[2(x+y)]2=(2x)2
解得,x=5y或x=y(不合题意舍去)
∵![]()
∴xy=36
在Rt![]() 中,BM2=x2—(x-y)2
中,BM2=x2—(x-y)2
在Rt![]() 中,BD2=x2-(x-y)2+y2=2xy
中,BD2=x2-(x-y)2+y2=2xy
∴BD2=72,
∴BD=6![]()
故答案为:6![]()

练习册系列答案
相关题目