题目内容
14.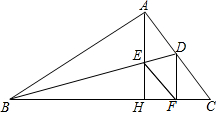 已知,在Rt△ABC中,∠BAC=90°,∠ABC的角平分线交AC于点D,AH⊥BC于H,交BD于E,DF⊥BC于F,求证:四边形AEFD为菱形.
已知,在Rt△ABC中,∠BAC=90°,∠ABC的角平分线交AC于点D,AH⊥BC于H,交BD于E,DF⊥BC于F,求证:四边形AEFD为菱形.
分析 根据全等三角形的判定定理HL进行证明Rt△BDF≌Rt△BDA(HL),得到∠ADE=∠FDE;根据平行线的性质、角平分线的性质以及等量代换推知∠EDA=∠AED,易证AD=AE;从而根据邻边相等的平行四边形是菱形进行判断.
解答  证明:∵∠BAC=90°,
证明:∵∠BAC=90°,
∴AC⊥EC.
又∵AD⊥AB,BD是∠ABC的平分线,
∴FD=AD.
在Rt△BDF与Rt△BDA中,
$\left\{\begin{array}{l}{FD=AD}\\{BD=BD}\end{array}\right.$,
∴Rt△BDF≌Rt△BDA(HL);
∴∠ADE=∠FDE,
∵AH是BC边上的高,
∴AH⊥BC.
又∵DF⊥BC,
∴AH∥DF,
∴∠AED=∠FDE.
∴∠EDA=∠AED,
∴AD=AE,
∴AD=DF=AE.
又∵DF∥AD,
∴四边形AEFD是菱形.
点评 本题考查了菱形的判定、全等三角形的判定与性质等知识点.菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
2.某校九年级数学兴趣小组的活动课题是“测量物体高度”.小组成员小明与小红分别采用不同的方案测量同一个底面为圆形的古塔高度,以下是他们研究报告的部分记录内容:
(1)写出小红研究报告中“计算古塔高度”的解答过程;
(2)数学老师说小红的结果较准确,而小明的结果与古塔的实际高度偏差较大.针对小明的测量方案分析测量发生偏差的原因;
(3)利用小明与小红的测量数据,估算该古塔底面圆直径的长度为8.4m.
| 课题:测量古塔的高度 | ||
| 小明的研究报告 | 小红的研究报告 | |
| 图示 | 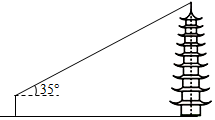 | 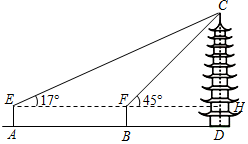 |
| 测量方案与测量数据 | 用距离地面高度为1.6m的测角器测出古塔顶端的仰角为35°,再用皮尺测得测角器所在位置与古塔底部边缘的最短距离为30m. | 在点A用距离地面高度为1.6m的测角器测出古塔顶端的仰角为17°,然后沿AD方向走58.8m到达点B,测出古塔顶端的仰角为45°. |
| 参考数据 | sin35°≈0.57,cos35°≈0.82,tan35°≈0.70 | sin17°≈0.29,cos17°≈0.96,tan17°≈0.30,$\sqrt{2}$≈1.41 |
| 计算古塔高度 (结果精确到0.1m) | 30×tan35°+1.6≈22.6(m) | |
(2)数学老师说小红的结果较准确,而小明的结果与古塔的实际高度偏差较大.针对小明的测量方案分析测量发生偏差的原因;
(3)利用小明与小红的测量数据,估算该古塔底面圆直径的长度为8.4m.
9.首都国际机场连续五年排名全球最繁忙机场第二位,该机场2012-2016年客流量统计结果如表:
根据统计表中提供的信息,预估首都国际机场2017年客流量约9823万人次,你的预估理由是由之前连续3年增长率预估2017年客流量的增长率约为4.5%.
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 客流量(万人次) | 8192 | 8371 | 8613 | 8994 | 9400 |
1.有一个两位数$\overrightarrow{ab}$,互换两位数的数字顺序,得到两位数$\overrightarrow{ba}$,若这两个两位数和等于99,则所有满足条件的原两位数的和是396.
 在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足$\left\{\begin{array}{l}{3a-b+2c=8}\\{a-2b-c=-4}\end{array}\right.$.
在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足$\left\{\begin{array}{l}{3a-b+2c=8}\\{a-2b-c=-4}\end{array}\right.$.