题目内容
13．11月橙子成熟，某水果店第一次用800元购进了一批橙子，并很快卖完．第二次又用750元，购进了同样的橙子，但第二次每千克的橙子是第一次进价的1.25倍，购进数量比第一次少50千克．（1）求水果店第一次购进这种橙子每干克的价格是多少元？
（2）12月，批发市场这种橙子的数量有所增加，该水果店所购进的数量比11月所购进的总量增加4a%，每千克进价在11月第一次进价的基础上上涨5a%，结果12月进货总价比11月进货总价多550元，求a的值．
分析 （1）设水果店第一次购进这种橙子每干克的价格是x元，则第二次购进这种橙子每千克的价格是1.25x元，根据数量=总价÷单价结合第二次购进的数量比第一次少50千克，即可得出关于x的分式方程，解之并检验后即可得出结论；
（2）根据数量=总价÷单价求出11月份购买的橙子数量，再根据单价×数量=总价结合12月进货总价比11月进货总价多550元，即可得出关于a的一元二次方程，解之即可得出结论．
解答 解：（1）设水果店第一次购进这种橙子每干克的价格是x元，则第二次购进这种橙子每千克的价格是1.25x元，
根据题意得：$\frac{800}{x}$-$\frac{750}{1.25x}$=50，
解得：x=4，
经检验，x=4是原方程的解，且符合题意．
答：水果店第一次购进这种橙子每干克的价格是4元．
（2）11月份购进橙子800÷4×2-50=350（千克）．
根据题意得：350（1+4a%）×4（1+5a%）=800+750+550，
整理得：40（a%）2+18a%-1=0，
解得：a%=$\frac{1}{20}$或a%=-$\frac{1}{2}$（舍去），
∴a=5．
答：a的值为5．
点评 本题考查了分式方程的应用以及一元二次方程的应用，解题的关键是：（1）根据数量=总价÷单价结合第二次购进的数量比第一次少50千克，列出关于x的分式方程；（2）根据单价×数量=总价结合12月进货总价比11月进货总价多550元，列出关于a的一元二次方程．
练习册系列答案
相关题目
5．在函数y=$\frac{\sqrt{x+1}}{x-2}$中，自变量x的取值范围是（ ）
| A． | x＞-1 | B． | x≥-1 | C． | x≥-1且x≠2 | D． | x＞-1且x≠2 |
1．现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿，两家鸡腿的价格相同，品质相近．快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿．检查人员从两家的鸡腿中各随机抽取15个，记录它们的质量（单位：g）如表所示．
根据表中数据，回答下列问题：
（1）甲厂抽取质量的中位数是75g；乙厂抽取质量的众数是75g．
（2）如果快餐公司决定从平均数和方差两方面考虑选购，现已知抽取乙厂的样本平均数$\overline{x}$乙=75，方差S${\;}_{乙}^{2}$≈1.86．请你帮助计算出抽取甲厂的样本平均数及方差（结果保留小数点后两位），并指出快餐公司应选购哪家加工厂的鸡腿？
| 质量（g） | 73 | 74 | 75 | 76 | 77 | 78 |
| 甲的数量 | 2 | 4 | 4 | 3 | 1 | 1 |
| 乙的数量 | 2 | 3 | 6 | 2 | 1 | 1 |
（1）甲厂抽取质量的中位数是75g；乙厂抽取质量的众数是75g．
（2）如果快餐公司决定从平均数和方差两方面考虑选购，现已知抽取乙厂的样本平均数$\overline{x}$乙=75，方差S${\;}_{乙}^{2}$≈1.86．请你帮助计算出抽取甲厂的样本平均数及方差（结果保留小数点后两位），并指出快餐公司应选购哪家加工厂的鸡腿？
8．
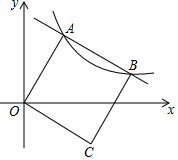如图，平面直角坐标系中，O为坐标原点，正方形OABC的定点A，B都在反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象上，边BC与x轴交于点D，则$\frac{BD}{CD}$的值为（ ）
如图，平面直角坐标系中，O为坐标原点，正方形OABC的定点A，B都在反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象上，边BC与x轴交于点D，则$\frac{BD}{CD}$的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
