Question

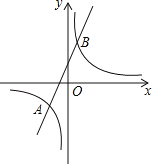
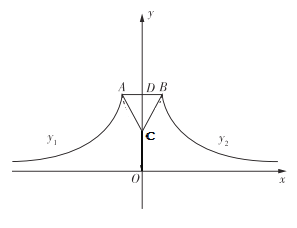
【题目】如图，小明用图形计算器绘制了如图所示的关于轴对称的图形，该图形由左右两侧的两段反比例函数图象和构成，点恰为的中点，．

求左右两侧反比例函数的关系式(要求分别注明自变量的取值范围)；

平行于轴的直线与该图形有三个交点，请求出交点坐标；

请分别写出直线与该图形有两个交点和没有交点时的取值范围．

Answer 1

【答案】（1）；（2）和；（3）有两个交点时：；没有交点时：或．

【解析】

（1）连接OA,OB，根据点是的中点，图形关于轴对称，，得到，再根据，得到，即可求解.

（2）根据平行于轴的直线与该图形有三个交点，得出直线经过点，分别令即可求解.

（3）直接看图即可求解.

如图，连接

点是的中点，图形关于轴对称，，

点在第二象限，点在第一象限，

平行于轴的直线与该图形有三个交点，

直线经过点

分别令得，

交点坐标为和．

有两个交点时：；

没有交点时：或．