ƒøƒĞ»ı
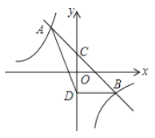
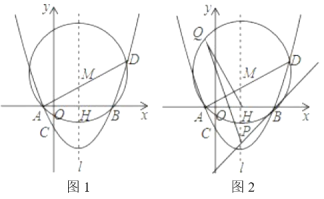
°æƒø°ø»ÁÕº1£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœşy![]() x2bxcΩªx÷·”е„A£¨B£¨µ„Bµƒ◊¯±ÍŒ™(4£¨0)£¨”Îy÷·”ĞΩª”е„C(0£¨©Å2)£Æ
x2bxcΩªx÷·”е„A£¨B£¨µ„Bµƒ◊¯±ÍŒ™(4£¨0)£¨”Îy÷·”ĞΩª”е„C(0£¨©Å2)£Æ
£®1£©«Û¥À≈◊ŒÔœşµƒΩ‚Œˆ Ω£ª
£®2£©‘Ğ≈◊ŒÔœş…œ»°µ„D£¨»Ùµ„Dµƒ∫·◊¯±ÍŒ™5£¨«Ûµ„Dµƒ◊¯±Íº∞°œADBµƒ∂» ˝£ª
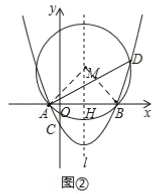
£®3£©‘Ğ£®2£©µƒÃº˛œ¬£¨…Ë≈◊ŒÔœş∂‘≥∆÷·![]() Ωªx÷·”е„H£¨°˜ABDµƒÕ‚Ω”‘≤‘≤–ƒŒ™M£®»ÁÕº1£©£¨
Ωªx÷·”е„H£¨°˜ABDµƒÕ‚Ω”‘≤‘≤–ƒŒ™M£®»ÁÕº1£©£¨
¢Ÿ«Ûµ„Mµƒ◊¯±Íº∞°—Mµƒ∞Îæ∂£ª
¢Ğπ˝µ„B◊˜°—Mµƒ«–œşΩª![]() ”е„P£®»ÁÕº2£©£¨…ËQŒ™°—M…œ“ª∂ص„£¨‘ڑе„Q‘À∂Øπ˝≥Ã÷–
”е„P£®»ÁÕº2£©£¨…ËQŒ™°—M…œ“ª∂ص„£¨‘ڑе„Q‘À∂Øπ˝≥Ã÷–![]() µƒ÷µ «∑Ò±‰ªØ£ø»Ù≤ª±‰£¨«Û≥ˆ∆‰÷µ£ª»Ù±‰ªØ£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ÷µ «∑Ò±‰ªØ£ø»Ù≤ª±‰£¨«Û≥ˆ∆‰÷µ£ª»Ù±‰ªØ£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©µ„
£ª£®2£©µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨45°„£ª£®3£©¢Ÿµ„
£¨45°„£ª£®3£©¢Ÿµ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨
£¨![]() µƒ∞Îæ∂Œ™
µƒ∞Îæ∂Œ™![]() £ª¢Ğ‘е„
£ª¢Ğ‘е„![]() ‘À∂Øπ˝≥Ã÷–
‘À∂Øπ˝≥Ã÷–![]() µƒ÷µ≤ª±‰£¨∆‰÷µŒ™
µƒ÷µ≤ª±‰£¨∆‰÷µŒ™![]()
°æΩ‚Œˆ°ø
£®1£©Ω´![]() £¨
£¨![]() ¥˙»ÎΩ‚Œˆ Ω£¨«Û≥ˆΩ‚Œˆ Ωµƒœµ ˝£¨º¥ø…µ√Ω‚£ª
¥˙»ÎΩ‚Œˆ Ω£¨«Û≥ˆΩ‚Œˆ Ωµƒœµ ˝£¨º¥ø…µ√Ω‚£ª
£®2£©Ω´![]() ¥˙»ÎΩ‚Œˆ Ω£¨«Û≥ˆ
¥˙»ÎΩ‚Œˆ Ω£¨«Û≥ˆ![]() £¨ø…µ√
£¨ø…µ√![]() µ„◊¯±Í£ª¡Ó
µ„◊¯±Í£ª¡Ó![]() £¨«Û≥ˆA°¢B◊¯±Í£¨”…π¥π…∂®¿ÌªÚ¡Ωµ„º‰æ‡¿Îπ´ Ω«Û≥ˆAD°¢BD£¨‘Ÿ”…√ʪ˝∑®«Û≥ˆBH£¨¥”∂¯«Û≥ˆ°œADBµƒ’˝œ“÷µ£¨ø…÷™°œADBµƒ∂» ˝£ª
£¨«Û≥ˆA°¢B◊¯±Í£¨”…π¥π…∂®¿ÌªÚ¡Ωµ„º‰æ‡¿Îπ´ Ω«Û≥ˆAD°¢BD£¨‘Ÿ”…√ʪ˝∑®«Û≥ˆBH£¨¥”∂¯«Û≥ˆ°œADBµƒ’˝œ“÷µ£¨ø…÷™°œADBµƒ∂» ˝£ª
£®3£©¢Ÿ”…‘≤÷İΩ«∂®¿ÌΩ·∫œµ»—¸÷±Ω«»˝Ω«–Œ±şµƒπÿœµ«Û≥ˆµ„![]() µƒ◊¯±Í∫Õ°—
µƒ◊¯±Í∫Õ°—![]() µƒ∞Îæ∂£ª¢Ğ÷§√˜QH∫ÕQPÀ˘‘еƒ°˜HMQ∫Õ°˜QMPœ‡À∆º¥ø…£Æ
µƒ∞Îæ∂£ª¢Ğ÷§√˜QH∫ÕQPÀ˘‘еƒ°˜HMQ∫Õ°˜QMPœ‡À∆º¥ø…£Æ
£®1£©Ω´![]() £¨
£¨![]() ¥˙»ÎΩ‚Œˆ Ωµ√£¨
¥˙»ÎΩ‚Œˆ Ωµ√£¨![]() £¨
£¨![]() £¨
£¨
°‡…Ë≈◊ŒÔœşµƒΩ‚Œˆ ΩŒ™£∫![]()
£®2£©µ±![]() ±£¨
±£¨![]()
°‡µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() ªÚ4£¨
ªÚ4£¨
°‡![]() £¨
£¨![]()
»ÁÕº£¨¡¨Ω·![]() £¨◊˜
£¨◊˜![]() ”Ğ
”Ğ![]() £¨
£¨

°ş![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°‡![]() £¨
£¨![]() £¨
£¨
°ş![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £ª
£ª
£®3£©¢Ÿ»ÁÕº£¨¡¨Ω”![]() £¨
£¨![]() £¨
£¨
°ş![]() £¨
£¨
°‡![]() £¨
£¨
°ş![]() £¨
£¨![]() £¨
£¨
°‡![]() £¨
£¨
°‡µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨°—
£¨°—![]() µƒ∞Îæ∂Œ™
µƒ∞Îæ∂Œ™![]() £ª
£ª
¢Ğ»ÁÕº£¨¡¨Ω”![]() £¨
£¨![]() £¨
£¨
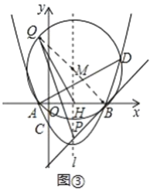
°şπ˝µ„![]() ◊˜°—
◊˜°—![]() µƒ«–œşΩª
µƒ«–œşΩª![]() ”е„
”е„![]() £¨
£¨
°‡![]() £¨
£¨
°ş![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°ş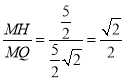 £¨
£¨
°‡![]() £¨
£¨
°ş![]() £¨
£¨
°‡![]() °◊
°◊![]() £¨
£¨
°‡ £¨
£¨
°‡‘е„![]() ‘À∂Øπ˝≥Ã÷–
‘À∂Øπ˝≥Ã÷–![]() µƒ÷µ≤ª±‰£¨∆‰÷µŒ™
µƒ÷µ≤ª±‰£¨∆‰÷µŒ™![]() £Æ
£Æ

 √˚–£¡∑øºæÌ∆Ѓ©≥Â¥ÃæÌœµ¡–¥∞∏
√˚–£¡∑øºæÌ∆Ѓ©≥Â¥ÃæÌœµ¡–¥∞∏