题目内容
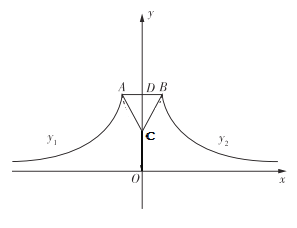
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,抛物线
,抛物线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,连结
,连结![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的表达式;
的表达式;
(3)设抛物线![]() 分别交边
分别交边![]() ,
,![]() 延长线于点
延长线于点![]() ,
,![]() .
.
①若![]() ,求抛物线表达式;
,求抛物线表达式;
②若![]() 与
与![]() 相似,则
相似,则![]() 的值为 .(直接写出答案)
的值为 .(直接写出答案)
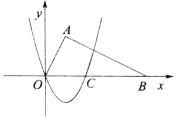
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() .
.
【解析】
(1)求得对称轴,由对称性可知C点坐标;
(2)利用待定系数法求解可得;
(3)①由AE=3AO的关系,建立K型模型相似,求得点E坐标代入解析式可得;
②若△CDB与△BOA相似,则∠OAB=∠CDB=90°,由相似关系可得点D坐标,代入解析式y=ax2-2ax可得a值.
解:(1)把![]() 代入
代入![]() ,得
,得![]() ,
,
解得:![]() ,或
,或![]() .
.
∵点![]() 在
在![]() 轴正半轴上,
轴正半轴上,
∴点![]() 的坐标为
的坐标为![]() .
.
(2)设直线表达式为![]() ,把点
,把点![]() ,
,![]() 分别代入
分别代入![]() ,
,
得![]() ,解得
,解得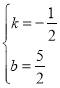 ,
,
∴直线![]() 的表达式为:
的表达式为:![]() .
.
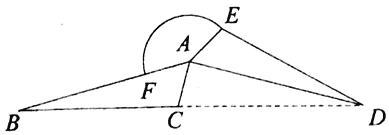
(3)①作![]() 轴于点
轴于点![]() ,
,![]() 于点
于点![]() (如图),
(如图),
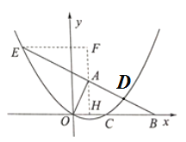
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
由![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 坐标为
坐标为![]() .
.
把![]() 代入
代入![]() ,得
,得![]() ,
,
解得:![]() .
.
∴![]() .
.
②若△CDB与△BOA相似,如图,作DG⊥BC,
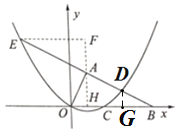
∴![]() ,∠OAB=∠CDB=90°,
,∠OAB=∠CDB=90°,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴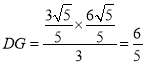 ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴点D的坐标为:(![]() ,
,![]() ),
),
把点D代入![]() ,即
,即![]()
解得:![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目