Question

【题目】已知矩形ABCD中，AB＝2，BC＝m，点E是边BC上一点，BE＝1，连接AE，沿AE翻折△ABE使点B落在点F处．

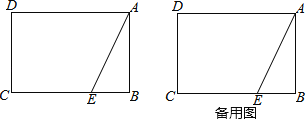
（1）连接CF，若CF∥AE，求m的值；

（2）连接DF，若≤DF≤，求m的取值范围．

Answer 1

【答案】（1）m的值是2；（2）

【解析】

（1）画出图形，由CF∥AE可得内错角和同位角相等，由翻折有对应角相等，等量代换后出现等腰三角形，即求出m的值．

（2）由于△ABE的形状大小是固定的，其翻折图形也固定，故可求点F到AD的距离FG与AG的长度，根据△DFG是直角三角形即可利用勾股定理用含m的式子表示DF2的长度，此时可把DF2看作是m的二次函数，根据二次函数图象的性质和DF2的范围，确定自变量m的范围．

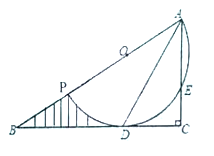
解：（1）①如图1，∵CF∥AE

∴∠FCE＝∠AEB，∠CFE＝∠AEF

∵△ABE翻折得到△AFE

∴EF＝BE＝1，∠AEF＝∠AEB

∴∠FCE＝∠CFE

∴CE＝EF＝1

∴m＝BC＝BE+CE＝2

∴m的值是2．

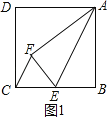
②如图2，过点F作GH⊥AD于点G，交BC于点H．

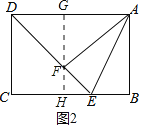
∴GH⊥BC

∴∠AGF＝∠FHE＝90°

∵四边形ABCD是矩形

∴∠BAD＝∠B＝90°

∴四边形ABHG是矩形

∴GH＝AB＝2，AG＝BH

∵△ABE翻折得到△AFE

∴EF＝BE＝1，AF＝AB＝2，∠AFE＝∠B＝90°

∴∠AFG+∠EFH＝∠AFG+∠FAG＝90°

∴∠EFH＝∠FAG

∴△EFH∽△FAG

∴＝＝＝，设EH＝x，则AG＝BH＝x+1

∴FG＝2EH＝2x

∴FH＝GH﹣FG＝2﹣2x

∴＝，

解得：x＝，

∴AG＝，FG＝，

∵AD＝BC＝m

∴DG＝|AD﹣AG|＝|m﹣|

∴DF2＝DG2+FG2＝（m﹣）2+（）2≥，

即可把DF2看作关于m的二次函数，抛物线开口向上，最小值为，

∵≤DF≤，

∴≤DF2≤，

∵（m﹣）2+（）2＝，

解得：m1＝，m2＝1

∴根据二次函数图象可知，1≤m≤．