题目内容
【题目】已知：抛物线y＝x2﹣2x+m与y轴交于点C（0，﹣2），点D和点C关于抛物线对称轴对称．
（1）求此抛物线的解析式和点D的坐标；
（2）如果点M是抛物线的对称轴与x轴的交点，求MCD的周长．
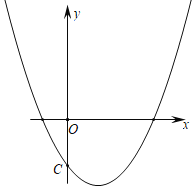
【答案】（1）y＝x2﹣2x﹣2，点D的坐标为（2，﹣2）；（2）2+2
．
【解析】
（1）利用二次函数图象上点的坐标特征可求出m值，进而可得出抛物线的解析式，由抛物线的解析式利用二次函数的性质可得出抛物线的对称轴，结合点C的坐标可得出点D的坐标；
（2）求得M点的坐标，然后根据勾股定理求得MC＝MD＝，即可求得△MCD的周长为：2+2．
（1）抛物线y＝x2﹣2x+m与y轴交于点C（0，﹣2），
∴m＝﹣2，
∴此抛物线的解析式为y＝x2﹣2x﹣2，
∵抛物线的解析式为y＝x2﹣2x﹣2＝（x﹣1）2﹣3，
∴抛物线的对称轴为直线x＝1．
∵点D与C关于抛物线的对称轴对称，
∴点D的坐标为（2，﹣2）．
（2）∵抛物线的对称轴为直线x＝1．
∴M（1，0），
∴MC＝MD＝
＝
∵CD＝2，
∴△MCD的周长为：2+2．
练习册系列答案
相关题目
