Question

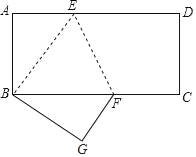
【题目】如图1，在矩形ABCD中，点E在CD上，∠AEB＝90°，点P从点A出发，沿A→E→B的路径匀速运动到点B停止，作PQ⊥CD于点Q，设点P运动的路程为x，PQ长为y，若y与x之间的函数关系图象如图2所示，当x＝6时，PQ的值是(　　)

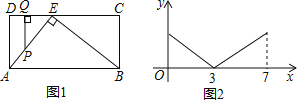
A. 2B. C. D. 1

Answer 1

【答案】B

【解析】

由图象可知：AE＝3，BE＝4，根据勾股定理可得AB=5,当x＝6时，点P在BE上，先求出PE的长，再根据PQEBAE，求出PQ的长．

解：由图象可知：

AE＝3，BE＝4，

在RtABE中，∠AEB＝90°

AB==5

当x＝6时，点P在BE上，如图,

此时PE=4-(7-x)=x-3=6-3=3

∵∠AEB＝90°, PQ⊥CD

∴∠AEB=∠PQE=90°,

在矩形ABCD中，AB//CD

∴∠QEP=∠ABE

∴PQEBAE, ∴=

∴ =

∴PQ=

故选：B．