题目内容
13.先化简,再求值:$\frac{{x}^{2}-4x+4}{{x}^{2}-2x}$+$\frac{1}{x}$,其中x=$\frac{1}{2}$.分析 首先化简$\frac{{x}^{2}-4x+4}{{x}^{2}-2x}$+$\frac{1}{x}$,然后把x=$\frac{1}{2}$代入化简后的算式,求出算式的值是多少即可.
解答 解:$\frac{{x}^{2}-4x+4}{{x}^{2}-2x}$+$\frac{1}{x}$
=$\frac{{(x-2)}^{2}}{x(x-2)}+\frac{1}{x}$
=$\frac{x-2}{x}+\frac{1}{x}$
=$\frac{x-1}{x}$
当x=$\frac{1}{2}$时,
$\frac{x-1}{x}=\frac{\frac{1}{2}-1}{\frac{1}{2}}=\frac{-\frac{1}{2}}{\frac{1}{2}}=-1$.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,解答此题的关键是要明确:(1)化简时不能跨度太大,而缺少必要的步骤.( 2)代入求值时,有直接代入法,整体代入法等常用方法.

练习册系列答案
相关题目
1. 如图所示的几何物体的左视图是( )
如图所示的几何物体的左视图是( )
 如图所示的几何物体的左视图是( )
如图所示的几何物体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
18.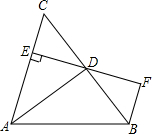 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.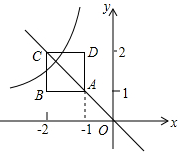 如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
 如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )| A. | -4≤k≤-1 | B. | -4<k<-1 | C. | -4≤k<-1 | D. | 1≤k≤4 |
3.为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
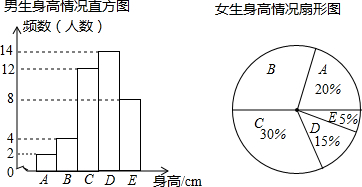
根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在D组(填组别序号),女生身高在B组的人数有12人;
(2)在样本中,身高在150≤x<155之间的人数共有16人,身高人数最多的在C组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?
| 组别 | 身高(cm) |
| A | x<150 |
| B | 150≤x<155 |
| C | 155≤x<160 |
| D | 160≤x<165 |
| E | x≥165 |

根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在D组(填组别序号),女生身高在B组的人数有12人;
(2)在样本中,身高在150≤x<155之间的人数共有16人,身高人数最多的在C组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?




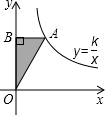 如图,已知A点是反比例函数y=$\frac{k}{x}$(k≠0)的图象上一点,AB⊥y轴于B,且△AOB的面积为2,则k的值为( )
如图,已知A点是反比例函数y=$\frac{k}{x}$(k≠0)的图象上一点,AB⊥y轴于B,且△AOB的面积为2,则k的值为( )